Square T-beam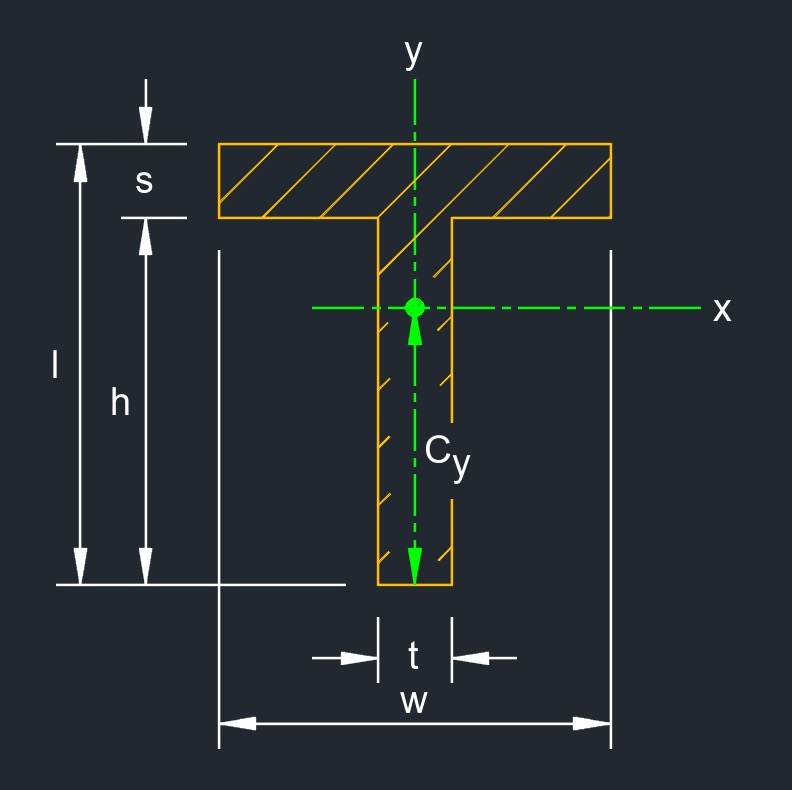, also called T-shaped beam or Tee beam, is a type of structural beam with a T-shaped cross-sectional profile. Unlike a standard I-beam that has a central vertical web and horizontal flanges at the top and bottom, a T-beam has a vertical stem and a horizontal flange extending from the stem at the top. This configuration creates a cross-sectional shape that resembles the letter "T." A Square T-beam is characterized by having equal-length stem and flange portions, resulting in a symmetrical T-shape. The stem and flange can have varying dimensions and thicknesses, depending on the specific load bearing requirements and design considerations of the structure.
- See Article - Geometric Properties of Structural Shapes
area of a Square T Beam formula |
||
| \( A \;=\; w\cdot s + h\cdot t \) | ||
| Symbol | English | Metric |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( s \) = width | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
Distance from Centroid of a Square T Beam formulas |
||
|
\( C_x \;=\; 0 \) \( C_y \;=\; \dfrac{ l^2\cdot t + s^2 \cdot \left( w - t \right) }{ 2\cdot \left( w\cdot s + h\cdot t \right) } \) |
||
| Symbol | English | Metric |
| \( C \) = distance from centroid | \( in \) | \( mm \) |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( s \) = width | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
Elastic section Modulus of a Square T Beam formulas |
||
|
\( S_{x} \;=\; \dfrac { I_{x} }{ C_{y} } \) \( S_{y} \;=\; \dfrac { I_{y} }{ C_{x} } \) |
||
| Symbol | English | Metric |
| \( S \) = elastic section modulus | \( in^3 \) | \( mm^3 \) |
| \( C \) = distance from centroid | \( in \) | \( mm \) |
| \( I \) = moment of inertia | \( in^4 \) | \( mm^4 \) |
Perimeter of a Square T Beam formula |
||
| \( P \;=\; 2\cdot \left( w + h + s \right) \) | ||
| Symbol | English | Metric |
| \( P \) = perimeter | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( s \) = width | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
Polar Moment of Inertia of a Square T Beam formulas |
||
|
\( J_{z} \;=\; I_{x} + I_{y}{^2} \) \( J_{z1} \;=\; I_{x1} + I_{y1}{^2} \) |
||
| Symbol | English | Metric |
| \( J \) = torsional constant | \( in^4 \) | \( mm^4 \) |
| \( I \) = moment of inertia | \( in^4 \) | \( mm^4 \) |
Radius of Gyration of a Square T Beam formulas |
||
|
\( k_{x} \;=\; \sqrt{ \dfrac{ I_{x} }{ A } } \) \( k_{y} \;=\; \sqrt{ \dfrac{ I_{y} }{ A } } \) \( k_{z} \;=\; \sqrt{ k_{x}{^2} + k_{y}{^2} } \) \( k_{x1} \;=\; \sqrt{ \dfrac{ I_{x1} }{ A } } \) \( k_{y1} \;=\; \sqrt{ \dfrac{ I_{y1} }{ A } } \) \( k_{z1} \;=\; \sqrt{ k_{x1}{^2} + k_{y1}{^2} } \) |
||
| Symbol | English | Metric |
| \( k \) = radius of gyration | \( in \) | \( mm \) |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( I \) = moment of inertia | \( in^4 \) | \( mm^4 \) |
Second Moment of Area of a Square T Beam formulas |
||
|
\( I_{x} \;=\; \dfrac{ t\cdot C_{y}{^3} + w \cdot \left( l - C_y \right)^3 - \left( w - t \right) \cdot \left( l - C_y - s \right)^3 }{3} \) \( I_{x} \;=\; \dfrac{ h\cdot t^3 }{12} + \dfrac{ w^3 \cdot s }{12} \) \( I_{x1} \;=\; I_{x} + A \cdot C_{y} \) \( I_{y1} \;=\; I_{y} + A\cdot C_{x} \) |
||
| Symbol | English | Metric |
| \( I \) = moment of inertia | \( in^4 \) | \( mm^4 \) |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( C \) = distance from centroid | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( s \) = width | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
Torsional Constant of a Square T Beam formula |
||
| \( J \;=\; \dfrac{ w\cdot s^3 + l - \left( \dfrac {s}{2} \right) \cdot t^3 }{3} \) | ||
| Symbol | English | Metric |
| \( J \) = torsional constant | \( in^4 \) | \( mm^4 \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( s \) = width | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
