HomeMathematicsGeometrySolid GeometryRight Hexagonal Prism
Print

Right Hexagonal Prism

on . Posted in Solid Geometry

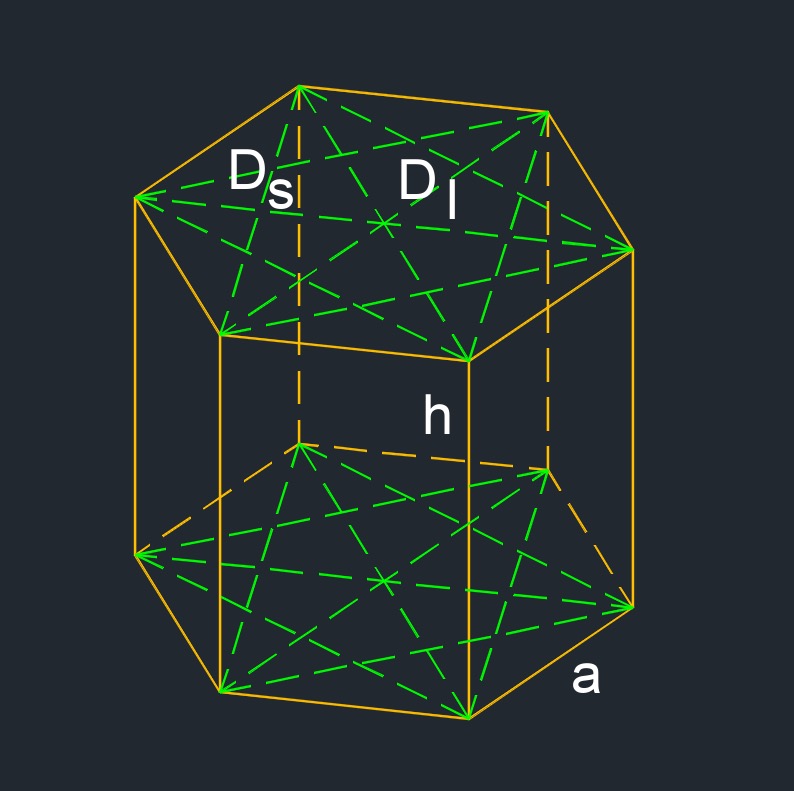
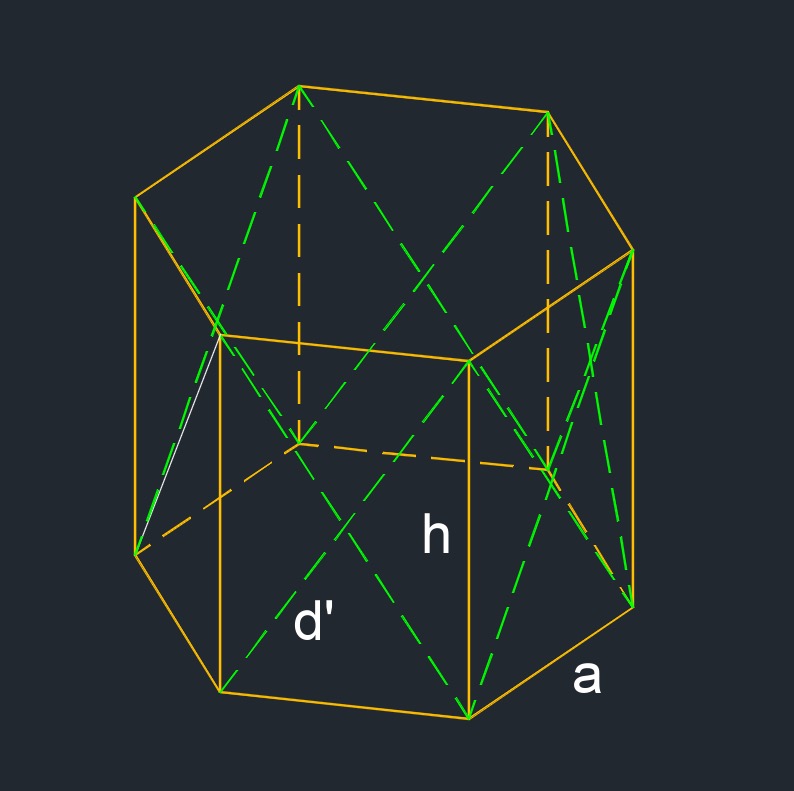
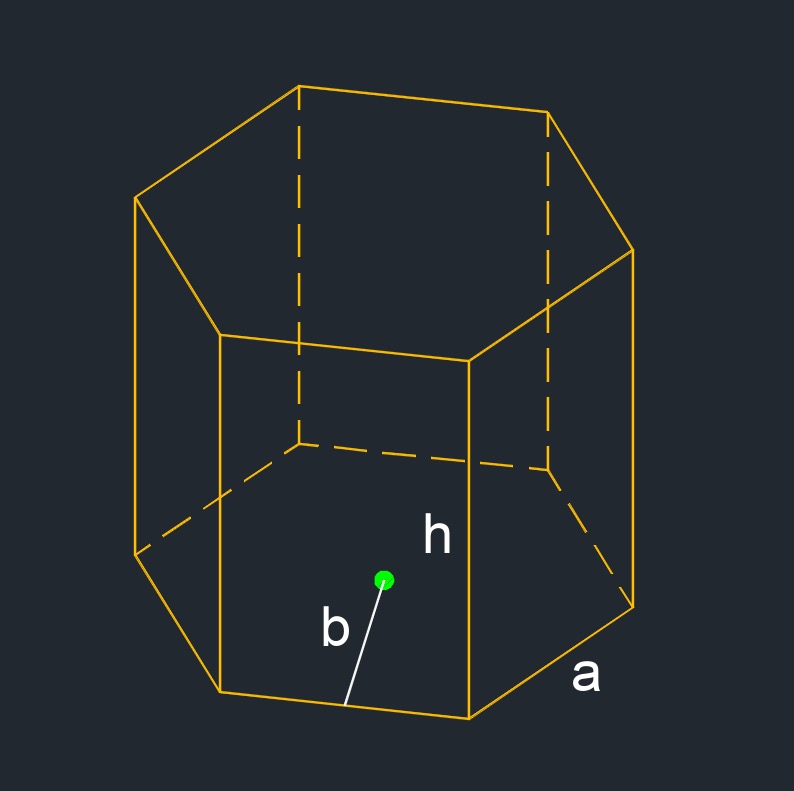  • hexagonal prism 2Right hexagon prism (a three-dimensional figure) is where each face is a regular polygon with equal sides and equal angles.
  • Long diagonal always crosses the center point of the hexagon.
  • Short diagonal does not cross the center point of the hexagon.
  • 36 base diagonals
  • 12 face diagonals
  • 36 space diagonals
  • 2 bases
  • 18 edges
  • 6 side faces
  • 12 vertexs

Right Hexagonal Prism Index

 

hexagonal prism 3

Base Area of a Right Hexagonal Prism formula
\(\large{ A_b = 3\; \sqrt {3}\; \frac { a^2 } { 2 }   }\) 
Symbol English Metric
\(\large{A_b }\) = base area \(\large{ in^2 }\)  \(\large{ mm^2 }\) 
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)

 

 

 

hexagonal prism 5

Base Long Diagonal of a Right Hexagon formula

Long diagonal always crosses the center point of the hexagon.
\(\large{ D_l = 2\;a }\) 
Symbol English Metric
\(\large{ D_l }\) = long diagonal \(\large{ in }\)  \(\large{ mm }\) 
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)

 

 

 

hexagonal prism 5

Base Short Diagonal of a Right Hexagon formula

Short diagonal does not cross the center point of the hexagon.
\(\large{ D_s = \sqrt{3}\;a }\) 
Symbol English Metric
\(\large{ D_s }\) = short diagonal \(\large{ in }\)  \(\large{ mm }\) 
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)

 

 

hexagonal prism 6

Side Diagonal of a Right Hexagonal Prism formula
\( \large{ d' = \sqrt { a^2 + h^2 }   }\) 
Symbol English Metric
\(\large{ d' }\) = diagonal \(\large{ in }\)  \(\large{ mm }\) 
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)
\(\large{ h }\) = height \(\large{ in }\) \(\large{ mm }\)

 

 

regular hexagonal prism volume 1

Edge of a Right Hexagonal Prism formulas

\(\large{ a = \frac { A_{l} } { 6\;h }   }\) 

\(\large{ a = 3^{1/4}\; \sqrt {2\; \frac { V } { 9\;h } } }\)

\(\large{ a = \frac{1}{3} \;  \sqrt { 3\;h^2   +   \sqrt {3}\; A_s   }   - \sqrt {3}\; \frac {h}{3} }\)

\(\large{ a = 3^{1/4}\; \sqrt {2\; \frac { A_b } { 9 } } }\)
Symbol English Metric
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)
\(\large{ A_b }\) = base area \(\large{ in^2 }\) \(\large{ mm^2 }\)
\(\large{ h }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ A_l }\) = lateral surface area \(\large{ in^2 }\) \(\large{ mm^2 }\)
\(\large{ A_s }\) = surface area \(\large{ in^2 }\) \(\large{ mm^2 }\)
\(\large{ V }\) = volume \(\large{ in^3 }\) \(\large{ mm^3 }\)

 

regular hexagonal prism volume 1

Height of a Right Hexagonal Prism formulas

\(\large{ h = 2\; \sqrt {3}\; \frac { V } { 9\;a^2 }   }\) 

\(\large{ h =   \frac {A_s} {6\;a } - \sqrt {3}\; \frac { a } {2 }   }\)
Symbol English Metric
\(\large{ h }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)
\(\large{ A_s }\) = surface area \(\large{ in^2 }\) \(\large{ mm^2 }\)
\(\large{ V }\) = volume \(\large{ in^3 }\) \(\large{ mm^3 }\)

 

regular hexagonal prism volume 1

Lateral Surface Area of a Right Hexagonal Prism formula
\(\large{ A_l = 6\;a\;h }\) 
Symbol English Metric
\(\large{ A_l }\) = lateral surface area \(\large{ in^2 }\) \(\large{ mm^2 }\)
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)
\(\large{ h }\) = height \(\large{ in }\) \(\large{ mm }\)

 

regular hexagonal prism volume 1

Surface Area of a Right Hexagonal Prism formula
\(\large{ A_s = 6\;a\;h + 3\; \sqrt 3\; a^2 }\) 
Symbol English Metric
\(\large{ A_s }\) = surface area \(\large{ in^2 }\) \(\large{ mm^2 }\)
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)
\(\large{ h }\) = height \(\large{ in }\) \(\large{ mm }\)



regular hexagonal prism volume 1

Volume of a Right Hexagonal Prism formulas

\(\large{ V = \frac{3\; \sqrt {3} }{ 2 }  \; a^2\;h     }\) 

\(\large{ V = 3 \; a \; b \; h     }\) 
Symbol English Metric
\(\large{ V }\) = volume \(\large{ in^3 }\) \(\large{ mm^3 }\)
\(\large{ b }\) = center \(\large{ in }\) \(\large{ mm }\)
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)
\(\large{ h }\) = height \(\large{ in }\) \(\large{ mm }\)

 

Piping Designer Logo 1

 

 

 

Tags: Volume Solid Prism

Latest Articles