HomeMathematicsGeometryPlane GeometrySquare Diamond
Print

Square Diamond

on . Posted in Plane Geometry

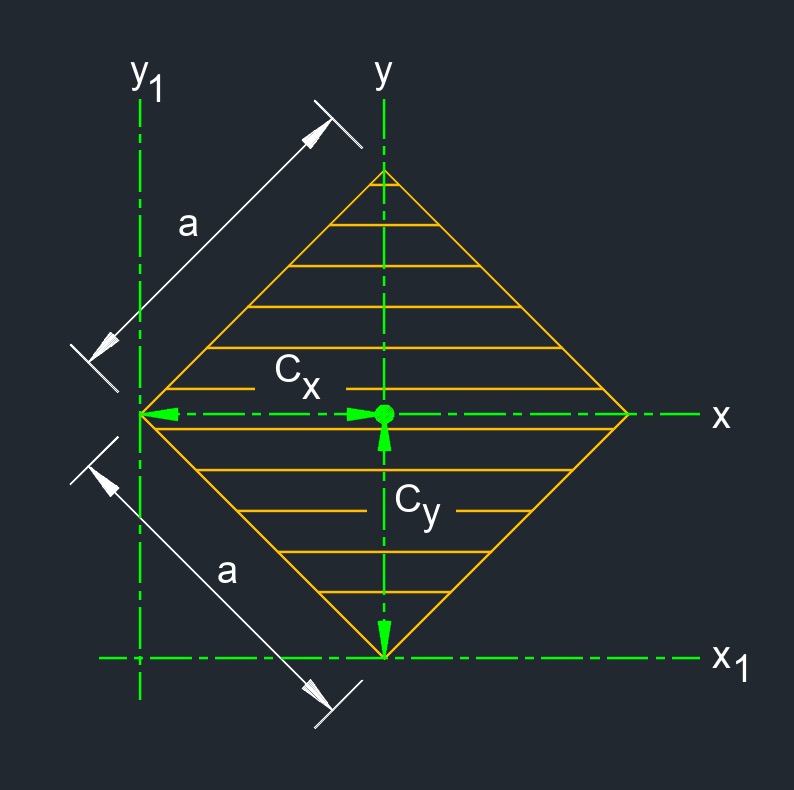  • square diamond 2A square diamond is a structural shape used in construction.
  • Abbreviated as SQ
  • Interior angles are 90°.
  • Exterior angles are 90°.
  • 2 diagonals
  • 4 edges
  • 4 vertexs

Square Diamond Index

 

Area of a Square Diamond formula
\(\large{ A = a^2 }\) 
Symbol English Metric
\(\large{ A_{area} }\) = area \(\large{ in^2 }\)  \(\large{ mm^2 }\)
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)

 

Distance from Centroid of a Square Diamond formulas

\(\large{ C_x =  \frac{ a }{ 2 }   }\)

\(\large{ C_y =  \frac{ a }{ 2}    }\)
Symbol English Metric
\(\large{ C }\) = distance from centroid \(\large{ in }\)  \(\large{ mm }\)
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)

   

Elastic Section Modulus of a Square Diamond formula
\(\large{ S =  \frac{ a^3 }{ 6\; \sqrt {2} }  }\) 
Symbol English Metric
\(\large{ S }\) = elastic section modulus \(\large{in^3}\)  \(\large{ mm^3 }\)
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)

 

Perimeter of a Square Diamond formulas
\(\large{ P= 4\;a  }\)
Symbol English Metric
\(\large{ P }\) = perimeter \(\large{ in }\)  \(\large{ mm }\)
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)

 

Plastic Section Modulus of a Square Diamond formula
\(\large{ Z =  \frac { a^3\; \sqrt {2} }  { 6  }  }\) 
Symbol English Metric
\(\large{ Z }\) = plastic section modulus \(\large{ in^3 }\)  \(\large{ mm^3 }\)
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)

  

Polar Moment of Inertia of a Square Diamond formulas

\(\large{ J_{z} = \frac{a^4}{6}  }\) 

\(\large{ J_{z1} =  \frac{2\;a^4}{3}  }\) 
Symbol English Metric
\(\large{ J }\) = torsional constant \(\large{ in^4 }\)  \(\large{ mm^4 }\)
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)

   

Radius of Gyration of a Square Diamond formulas

\(\large{ k_{x} =    \frac{ a }{  2 \; \sqrt{3}  }    }\) 

\(\large{ k_{y} =   \frac{ a }{  2 \; \sqrt{3}  }  }\) 

\(\large{ k_{z} =   \frac{ a }{  \sqrt{6}  }  }\) 

\(\large{ k_{x1} =   \frac{ a }{  \sqrt{3}  }  }\)

\(\large{ k_{y1} =   \frac{ a }{   \sqrt{3}  }  }\)

\(\large{ k_{z1} =   \sqrt{  \frac{2}{3} \;a }   }\)
Symbol English Metric
\(\large{ k }\) = radius of gyration \(\large{ in }\)  \(\large{ mm }\)
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)

 

Second Moment of Area of a Square Diamond formulas

\(\large{ I_{x} =  \frac{a^4}{12}  }\)

\(\large{ I_{y} = \frac{a^4}{12}  }\)

\(\large{ I_{x1} =   \frac{a^4}{3}  }\)

\(\large{ I_{y1} =  \frac{a^4}{3}  }\)
Symbol English Metric
\(\large{ I }\) = moment of inertia \(\large{ in^4 }\)  \(\large{ mm^4 }\)
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)

 

Side of a Square Diamond formula
\(\large{ a= \sqrt{A}   }\) 
Symbol English Metric
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)
\(\large{ A }\) = area \(\large{ in^2 }\)  \(\large{ mm^2 }\)

 

Torsional Constant of a Square Diamond formula
\(\large{ J  =  2.25  \;  \left(\frac{a}{2}\right)^4  }\) 
Symbol English Metric
\(\large{ J }\) = torsional constant \(\large{ in^4 }\)  \(\large{ mm^4 }\)
\(\large{ a }\) = edge \(\large{ in }\) \(\large{ mm }\)

 

Piping Designer Logo 1

Tags: Structural Steel

Latest Articles