HomeMathematicsGeometryPlane GeometryRotated Rectangle
Print

Rotated Rectangle

on . Posted in Plane Geometry

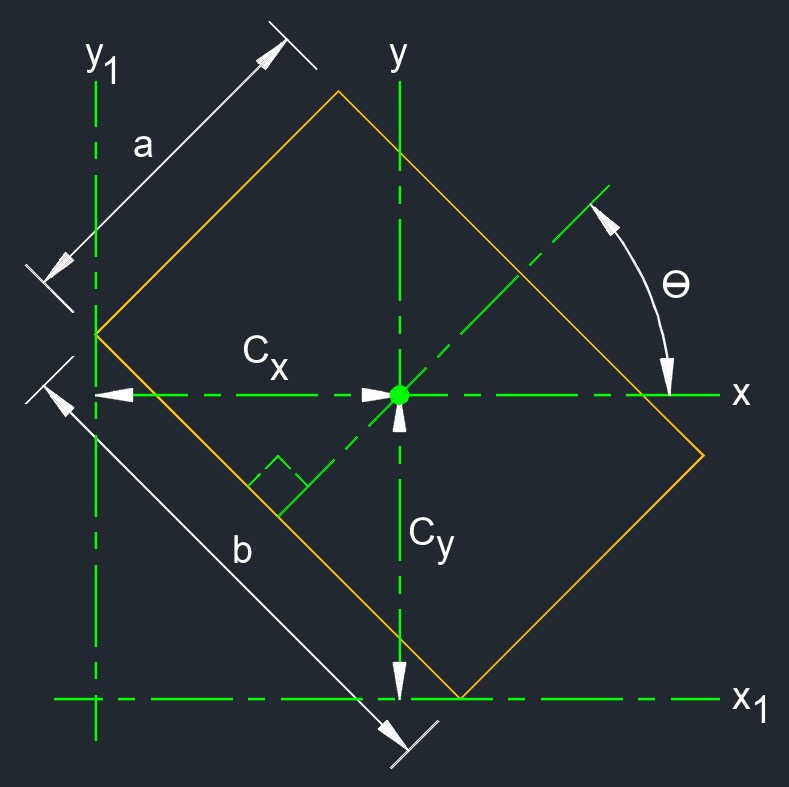  • rotated rectangle 2Rectangle is a quadrilateral with two pair of parallel lines.
  • A rotated rectangle is a structural shape used in construction.
  • Interior angles are 90°
  • Exterior angles are 90°
  • Angle \(\;A = B = C = D\)
  • 2 diagonals
  • 4 edges
  • 4 vertexs

Rotated Rectangle Index

 

 Area of a Rotated Rectangle formula

\( \large{ A_{area} = a \; b  }\)     (Area of a Rotated Rectangle)

\( \large{ a =  \frac{ A_{area} }{ b }  }\)

\( \large{ b =  \frac{ A_{area} }{ a }  }\) 
Symbol English Metric
\(\large{ A }\) = area \(\large{ in^2 }\)  \(\large{ mm^2 }\) 
\(\large{ a, b }\) = edge \(\large{ in }\) \(\large{ mm }\)

  

Distance from Centroid of a Rotated Rectangle formulas

\( \large{ C_x =  \frac {  b \; cos  \; \theta   \;+\;  a \; sin  \; \theta           }  { 2 }   }\)

\( \large{ C_y =  \frac {  a \; cos  \; \theta  \;+\;  b \; sin  \; \theta           }  { 2 }    }\) 
Symbol English Metric
\(\large{ C }\) = distance from centroid \(\large{ in^2 }\)  \(\large{ mm^2 }\) 
\(\large{ a, b }\) = edge \(\large{ in }\) \(\large{ mm }\)

 

Elastic Section Modulus of a Rotated Rectangle formula
\( \large{ S_x =  \frac{ b\;a\; \left(a^2 \; cos^2 \; \theta \;+\; b^2 sin^2\; \theta \right) }{ 6 \; \left( a \; cos\;\theta \;+\; b\;sin\;\theta\right) } }\) 
Symbol English Metric
\(\large{ S }\) = elastic section modulus \(\large{ in^3 }\)  \(\large{ mm^3 }\) 
\(\large{ a, b }\) = edge \(\large{ in }\) \(\large{ mm }\)

 

Perimeter of a Rotated Rectangle formula

\( \large{ P  =  2\; \left( a \;+\; b  \right)  }\)     (Perimeter of a Rotated Rectangle)

\( \large{ a  =  \frac{ P \;- \; 2 \; b }{ 2 }  }\)

\( \large{ b  =  \frac{ P \;- \; 2 \; a }{ 2 }  }\)
Symbol English Metric
\(\large{ P }\) = perimeter \(\large{ in }\)  \(\large{ mm }\) 
\(\large{ a, b }\) = edge \(\large{ in }\) \(\large{ mm }\)

 

Polar Moment of Inertia of a Rotated Rectangle formula
\(\large{ J_{z} = \frac{b\;a}{3} \; \left( b^2 \;+\; a^2  \right)        }\) 
Symbol English Metric
\(\large{ J }\) = torsional constant \(\large{ in^4 }\)  \(\large{ mm^4 }\) 
\(\large{ a, b }\) = edge \(\large{ in }\) \(\large{ mm }\)

 

Radius of Gyration of a Rotated Rectangle formula
\(\large{ k_{x} =    \sqrt{   \frac{  a^2 \;cos^2 \; \left(  b^2 \; sin^2 \; \theta  \;+\;  \theta  \right)    }{  2\;  \sqrt{3}  }    }      }\) 
Symbol English Metric
\(\large{ k }\) = radius of gyration \(\large{ in }\)  \(\large{ mm }\) 
\(\large{ a, b }\) = edge \(\large{ in }\) \(\large{ mm }\)

 

Second Moment of Area of a Rotated Rectangle formula
\(\large{ k_{x} =    \sqrt{   \frac{  a^2 \;cos^2 \; \left(  b^2 \; sin^2 \; \theta  \;+\;  \theta  \right)    }{  2\;  \sqrt{3}  }    }      }\) 
Symbol English Metric
\(\large{ I }\) = moment of inertia \(\large{ in^4 }\)  \(\large{ mm^4 }\) 
\(\large{ a, b }\) = edge \(\large{ in }\) \(\large{ mm }\)

 

Side of a Rotated Rectangle formulas

\( \large{ a = \frac{P}{2} - b   }\) 

\( \large{ b = \frac{P}{2} - a  }\) 
Symbol English Metric
\(\large{ P }\) = perimeter \(\large{ in }\)  \(\large{ mm }\) 
\(\large{ a, b }\) = edge \(\large{ in }\) \(\large{ mm }\)

 

Piping Designer Logo 1

Tags: Structural Steel

Latest Articles