Circle Corner
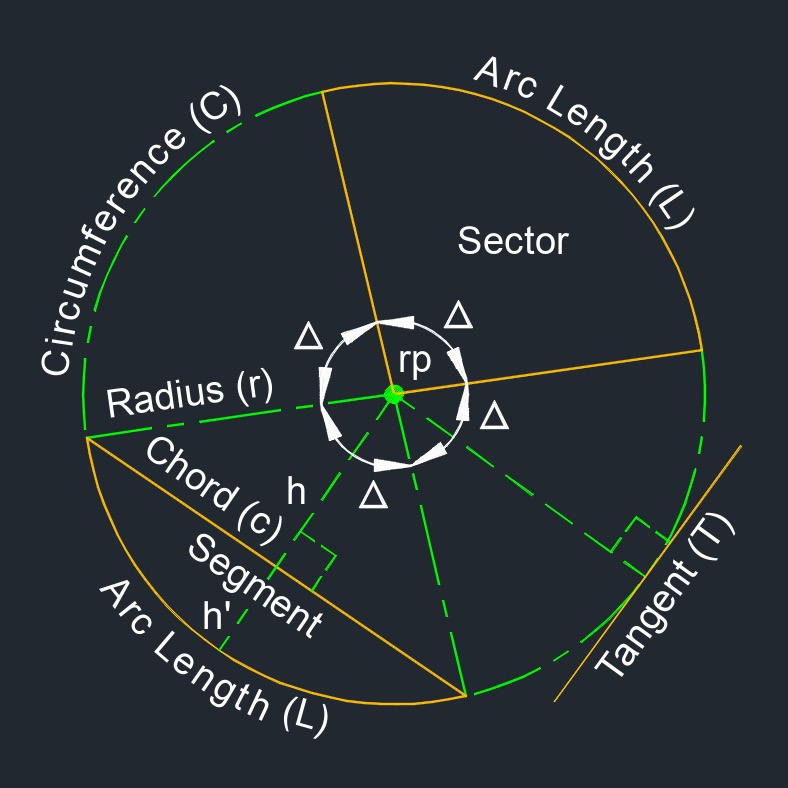
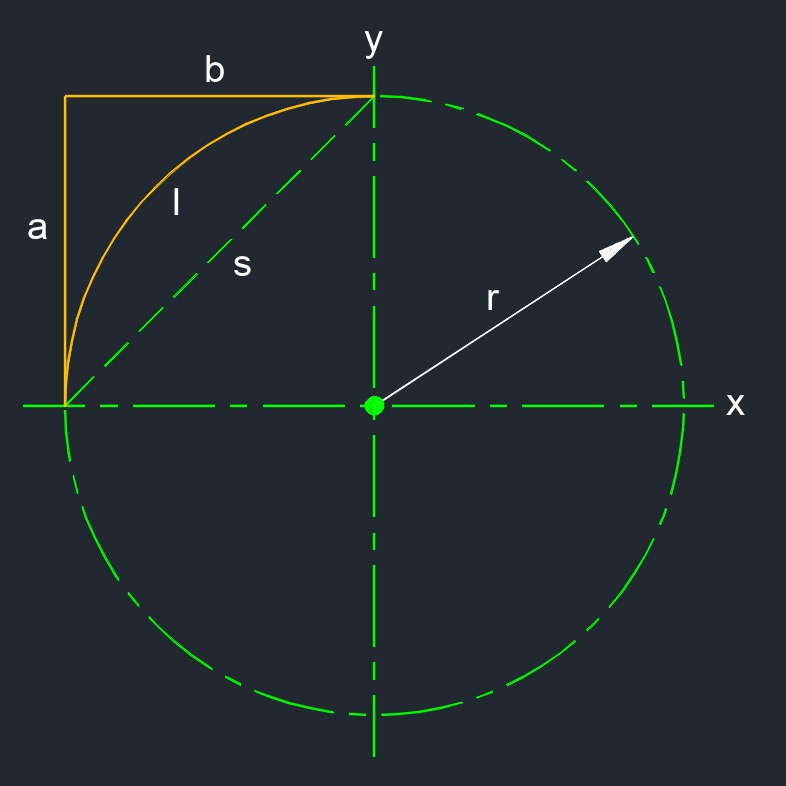 Circle corner (a two-dimensional figure) is a right triangle having acute vertices on a circle with the hypotenuse outside the circle.
Circle corner (a two-dimensional figure) is a right triangle having acute vertices on a circle with the hypotenuse outside the circle.- Chord is a line segment on the interior of a circle.
- Segment of a circle is an interior part of a circle bound by a chord and an arc.
Circle Corner Index
- Area of a Circle Corner
- Arc Length of a Circle Corner
- Chord Length of a Circle Corner
- Height of a Circle Corner
- Perimeter of a Circle Corner
- Segment Angle of a Circle Corner
Arc Length of a Circle Corner formula |
||
| \( L \;=\; r \; \Delta \) | ||
| Symbol | English | Metric |
| \( L \) = arc length | \(ft\) | \(m\) |
| \( \Delta \) = angle | \(deg\) | \(rad\) |
| \( r \) = radius | \(ft\) | \(m\) |
Chord Length of a Circle Corner formula |
||
| \( c \;=\; a^2 \; b^2 \) | ||
| Symbol | English | Metric |
| \( c \) = chord length | \(ft\) | \(m\) |
| \( a, b \) = edge | \(ft\) | \(m\) |
Perimeter of a Circle Corner formula |
||
| \( p \;=\; a + b + L \) | ||
| Symbol | English | Metric |
| \( p \) = perimeter | \(ft\) | \(m\) |
| \( L \) = arc length | \(ft\) | \(m\) |
| \( a, b \) = edge | \(ft\) | \(m\) |

Tags: Circle