Ellipse
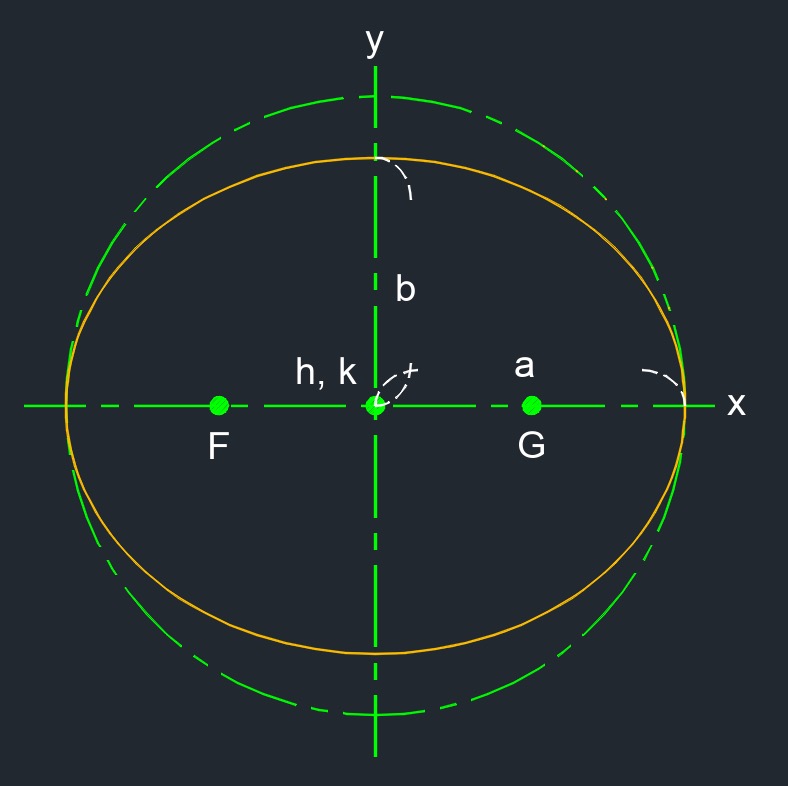
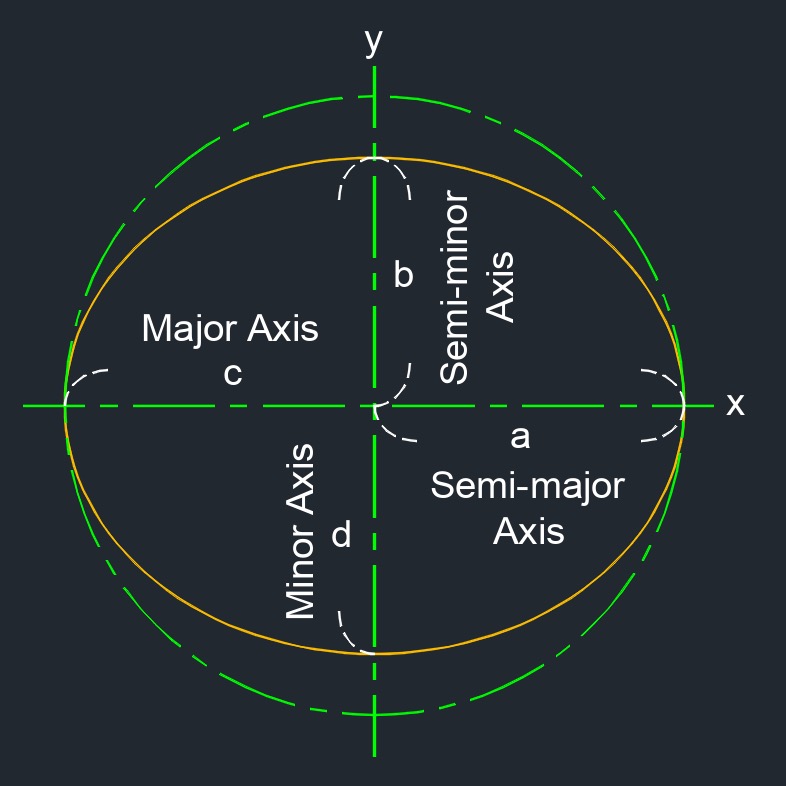Ellipse (a two-dimensional figure) is a conic section or a stretched circle. It is a flat plane curve that when adding togeather any two distances from any point on the ellipse to each of the foci will always equal the same.- Foci is a point used to define the conic section. F and G seperately are called "focus", both togeather are called "foci".
- The perimeter of an ellipse formula is an approximation that is about 5% of the true value as long as "a" is no more than 3 times longer than "b".
- Latus rectum is a line drawn perpencicular to the transverse axis of the ellipse and is passing through the foci of the ellipse.
- The major axis is always the longest axis in an ellipse.
- The minor axis is always the shortest axis in an ellipse.
Standard Ellipse formulas |
||
|
\(\large{ \frac {x^2}{a^2} + \frac {y^2}{x^2} = 1 }\) \(\large{ \left( \frac {x}{a} \right)^2 + \left( \frac {y}{x} \right)^2 = 1 }\) \(\large{ \frac { \left( x \;-\; h \right )^2 } { a^2 } + \frac { \left( y \;-\; k \right )^2 } { b^2 } = 1 }\) (major axis horizontal) \(\large{ \frac { \left( x \;-\; h \right )^2 } { b^2 } + \frac { \left( y \;-\; k \right )^2 } { a^2 } = 1 }\) (major axis vertical) |
||
| Symbol | English | Metric |
| \(\large{ x }\) = horizontal coordinate of a point on the ellipse | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ y }\) = vertical coordinate of a point on the ellipse | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a }\) = length semi-major axis | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ b }\) = length semi-minor axis | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ h }\) and \(\large{ k }\) = center point of ellipse | \(\large{ in }\) | \(\large{ mm }\) |
Area of an Ellipse formula |
||
| \(\large{ A = \pi \;a\; b }\) | ||
| Symbol | English | Metric |
| \(\large{ A }\) = area | \(\large{ in^2 }\) | \(\large{ mm^2 }\) |
| \(\large{ a }\) = length semi-major axis | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ b }\) = length semi-minor axis | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ \pi }\) = Pi | \(\large{3.141 592 653 ...}\) | |
Circumference of an Ellipse formula |
||
| \(\large{ C = 2\;\pi \; \sqrt{ \frac{ a^2 \;+\; b^2 }{ 2 } } }\) | ||
| Symbol | English | Metric |
| \(\large{ C }\) = circumference | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a }\) = length semi-major axis | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ b }\) = length semi-minor axis | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ \pi }\) = Pi | \(\large{3.141 592 653 ...}\) | |
eccentricity of an Ellipse formula |
||
|
\(\large{ \epsilon = \sqrt{ \frac{ a^2 \;-\; b^2 }{ a^2 } } }\) \(\large{ \epsilon = \left( \frac{ 1 \;-\; b^2 }{ a^2 } \right)^{0.5} }\) \(\large{ \epsilon = \sqrt{ 1 - \frac{ b^2 }{ a^2 } } }\) |
||
| Symbol | English | Metric |
| \(\large{ \epsilon }\) (Greek symbol epsilon) = eccentricity | \(\large{ dimensionless }\) | |
| \(\large{ a }\) = one half of the ellipse's major axis | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a }\) = one half of the ellipse's minor axis | \(\large{ in }\) | \(\large{ mm }\) |
This is an approximate perimeter of an ellipse formula. There is no easy way to calculate the ellipse perimeter with high accuracy.
Perimeter of an Ellipse formula |
||
|
\(\large{ p \approx 2\; \pi\; \sqrt { \frac{1}{2}\; \left(a^2 + b^2 \right) } }\) \(\large{ p \approx 2\; \pi\; \sqrt { \frac{a^2 \;+\; b^2}{2} } }\) |
||
| Symbol | English | Metric |
| \(\large{ p }\) = perimeter approximation | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a }\) = length semi-major axis | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ b }\) = length semi-minor axis | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ \pi }\) = Pi | \(\large{3.141 592 653 ...}\) | |
Latus Rectum of an Ellipse formula |
||
| \(\large{ L = \frac{ 2 \; b^2 }{ a } }\) | ||
| Symbol | English | Metric |
| \(\large{ L }\) = Latus rectum | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a }\) = length semi-major axis | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ b }\) = length semi-minor axis | \(\large{ in }\) | \(\large{ mm }\) |
Semi-major Axis Length of an Ellipse formula |
||
| \(\large{ a = \frac{A}{\pi \; b} }\) | ||
| Symbol | English | Metric |
| \(\large{ A }\) = area | \(\large{ in^2 }\) | \(\large{ mm^2 }\) |
| \(\large{ a }\) = length semi-major axis | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ b }\) = length semi-minor axis | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ \pi }\) = Pi | \(\large{3.141 592 653 ...}\) | |
Semi-minor Axis Length of an Ellipse formula |
||
| \(\large{ b = \frac{A}{\pi \; a} }\) | ||
| Symbol | English | Metric |
| \(\large{ A }\) = area | \(\large{ in^2 }\) | \(\large{ mm^2 }\) |
| \(\large{ a }\) = length semi-major axis | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ b }\) = length semi-minor axis | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ \pi }\) = Pi | \(\large{3.141 592 653 ...}\) | |
