Right Triangle
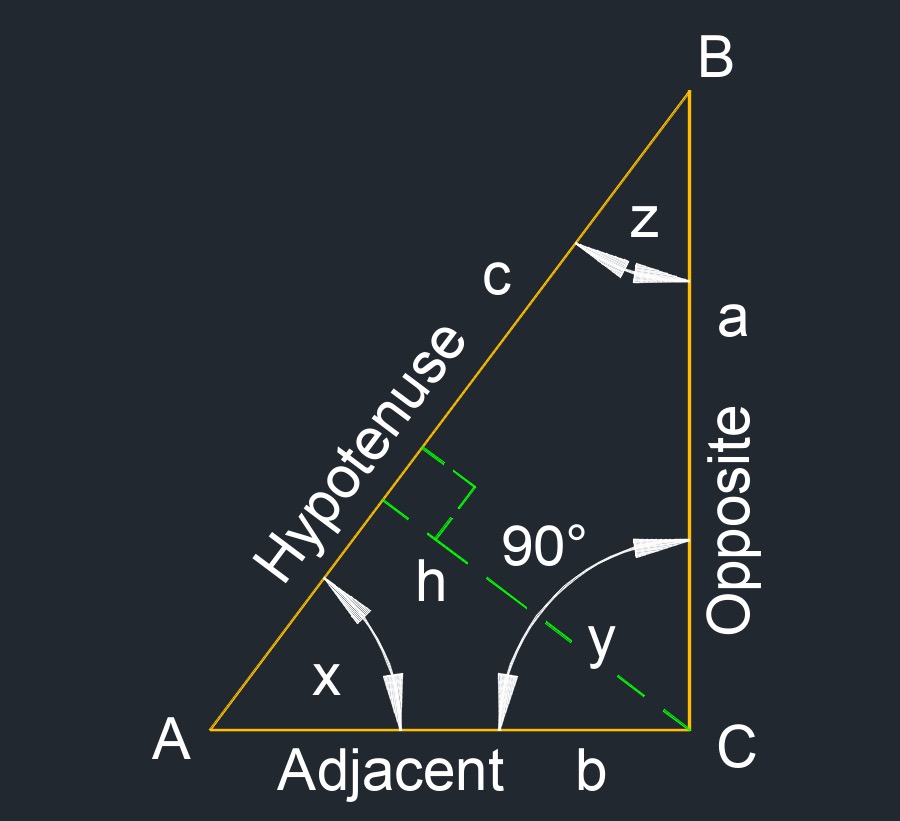 Right triangle (a two-dimensional figure) has one side a right 90° interior angle.
Right triangle (a two-dimensional figure) has one side a right 90° interior angle.- The other two angles are unequal and no sides are equal.
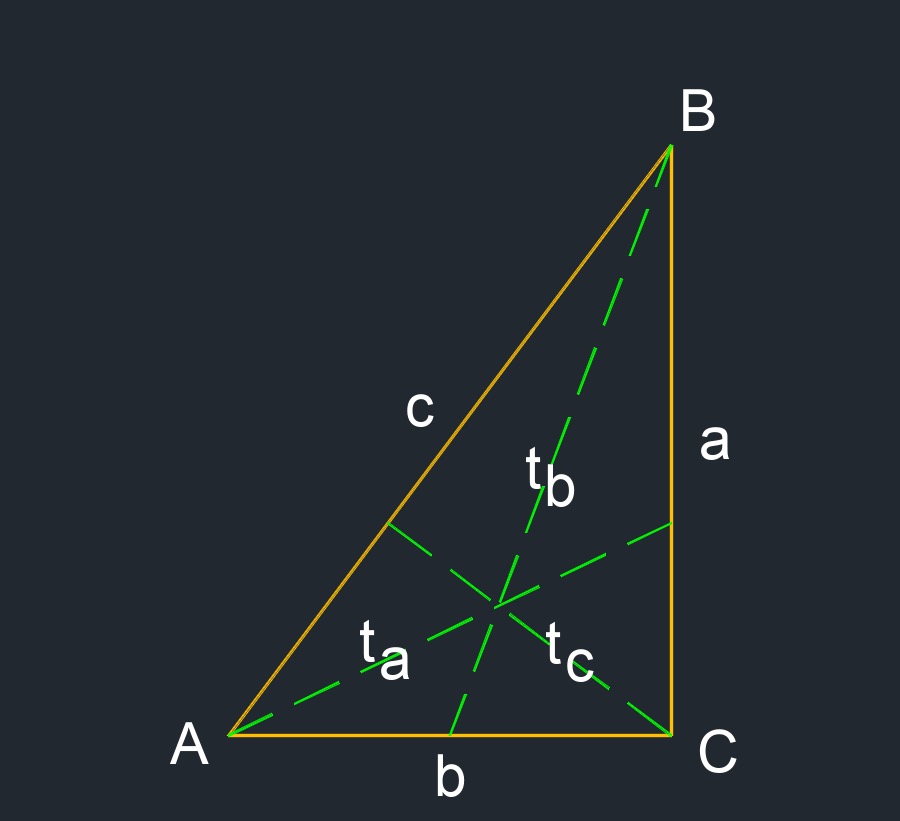
- Angle bisector of a right triangle is a line that splits an angle into two equal angles.
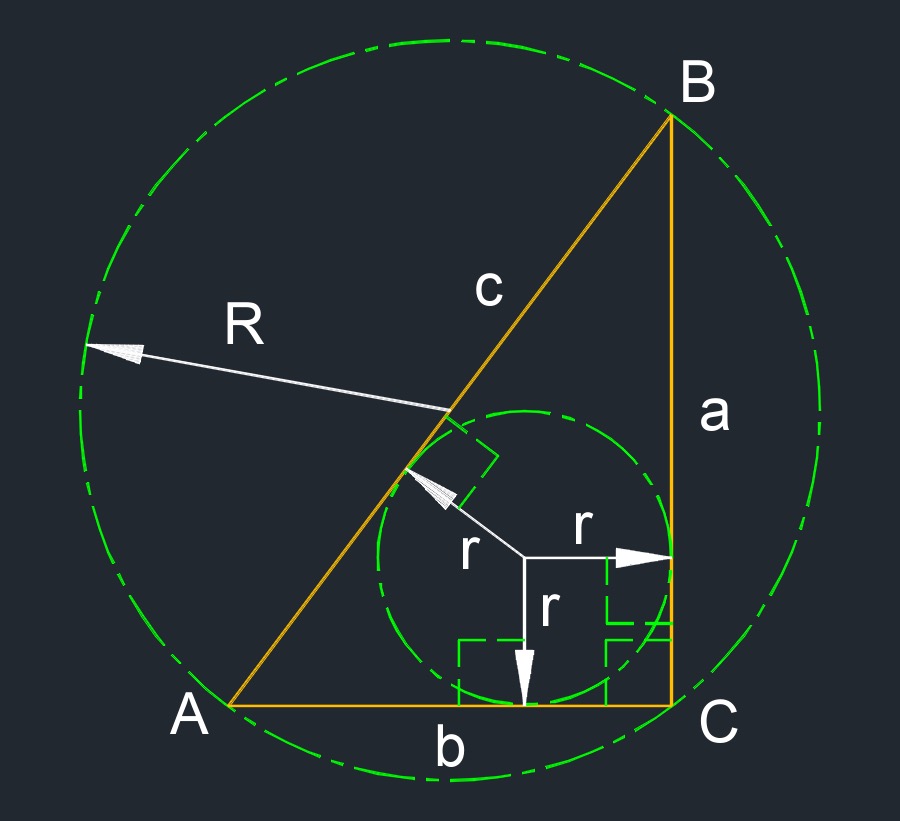
- Circumcircle is a circle that passes through all the vertices of a two-dimensional figure.
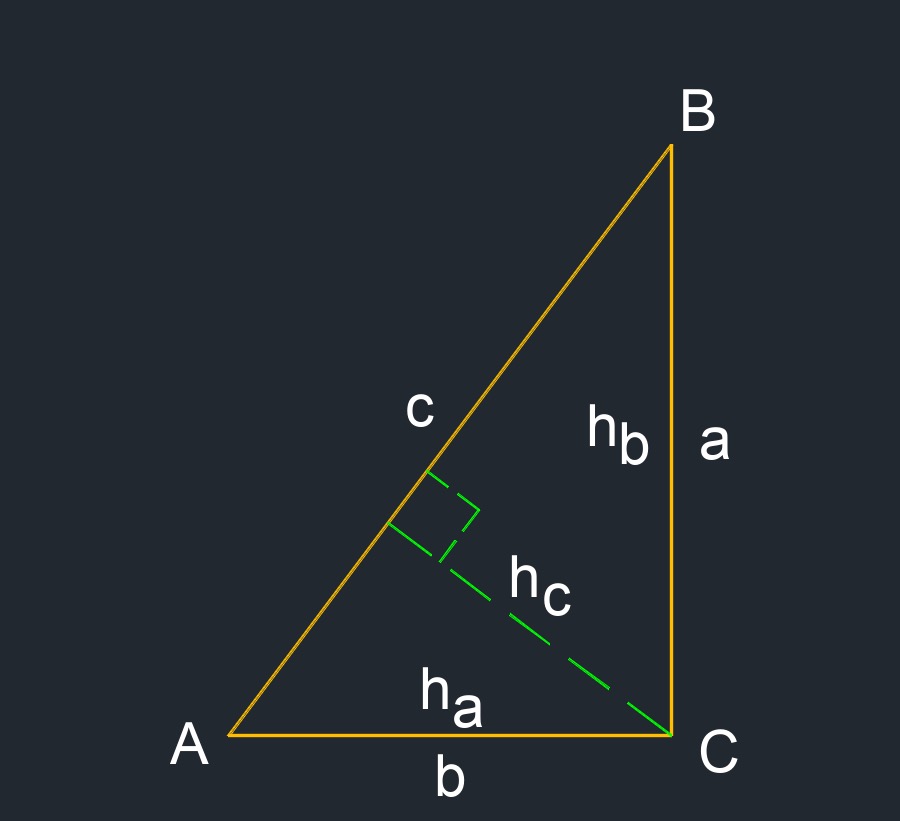
- Height of a right triangle is the length of the two sides and the perpendicular height of the 90 degree angle.
- Hypotenuse of a right triangle is the longest side or the side opposite the right angle.
- Inscribed circle is the largest circle possible that can fit on the inside of a two-dimensional figure.
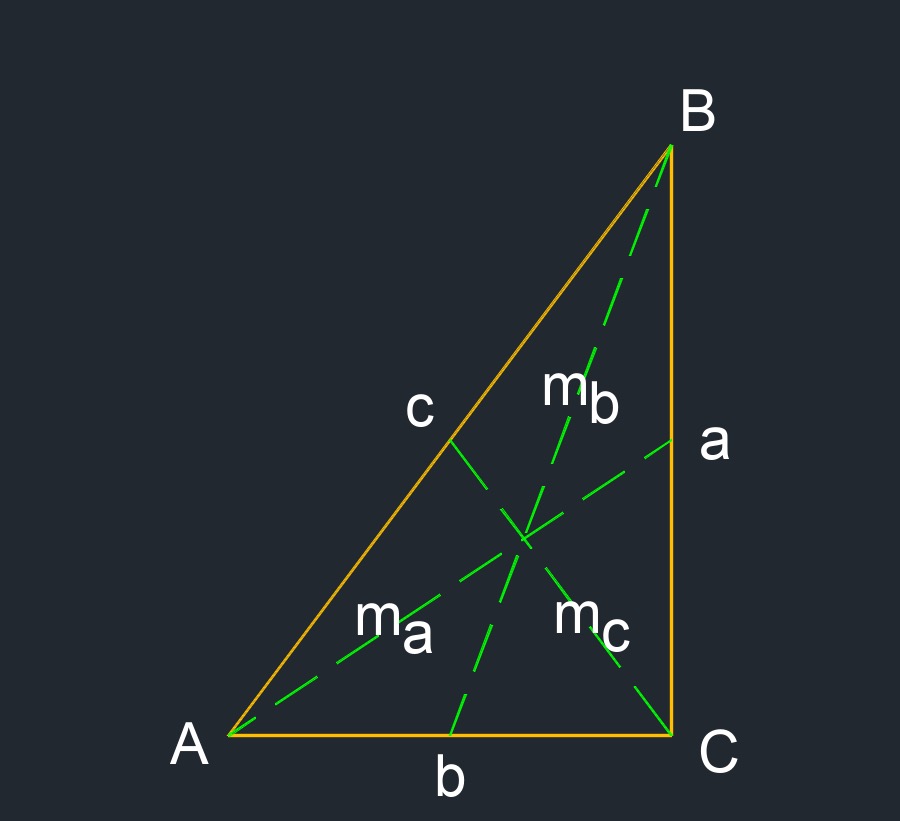
- Median of a right triangle is a line segment from a vertex (coiner point) to the midpoint of the opposite side.
- Semiperimeter is one half of the perimeter.
- 3 edges
- 3 vertexs
- a = opposite leg
- b = adjacent leg
- c = hypotenuse
- Angles: ∠A, ∠B, ∠C
- Height: \(h_a\), \(h_b\), \(h_c\)
- Median: \(m_a\), \(m_b\), \(m_c\) - A line segment from a vertex (coiner point) to the midpoint of the opposite side
- Angle bisectors: \(t_a\), \(t_b\), \(t_c\) - A line that splits an angle into two equal angles
Right Triangle Index
- Angle Bisector of a Right Triangle
- Area of a Right Triangle
- Circumcircle of a Right Triangle
- Height of a Right Triangle
- Hypotenuse of a Right Triangle
- Inscribed Circle of a Right Triangle
- Median of a Right Triangle
- Perimeter of a Right Triangle
- Semiperimeter of a Right Triangle
- Trig Functions

Tags: Triangle