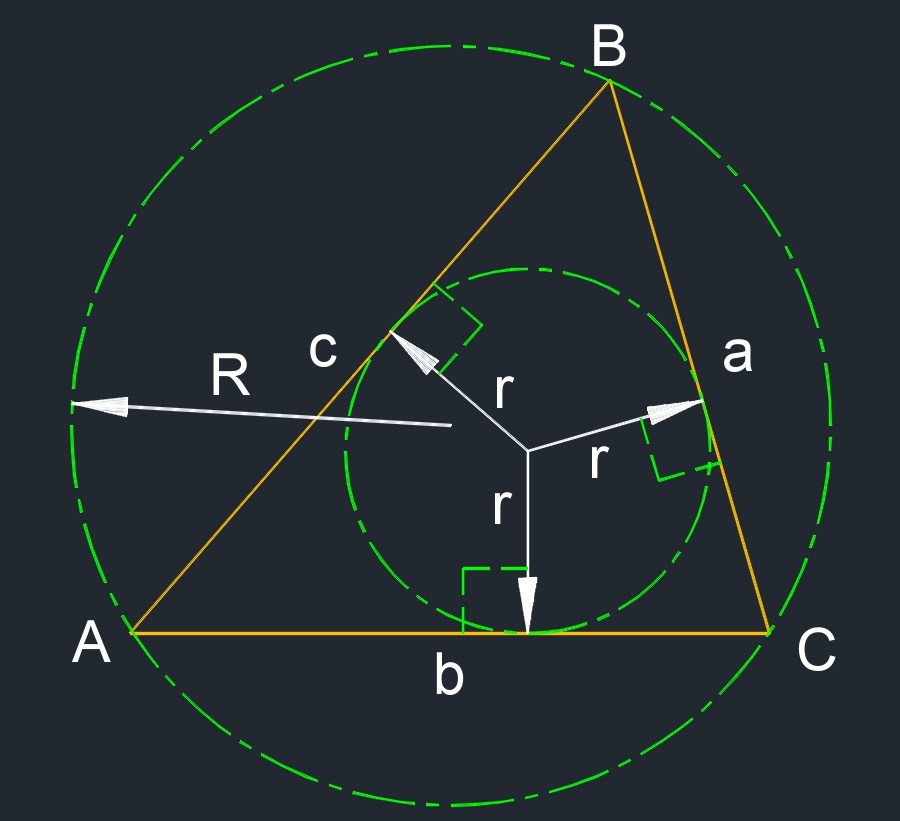
Scalene Triangle

on 29 January 2016. Posted in Plane Geometry

Scalene triangle (a two-dimensional figure) is where all three sides are different lengths and all three angles are different angles.
Angle bisector of a scalene triangle is a line that splits an angle into two equal angles.
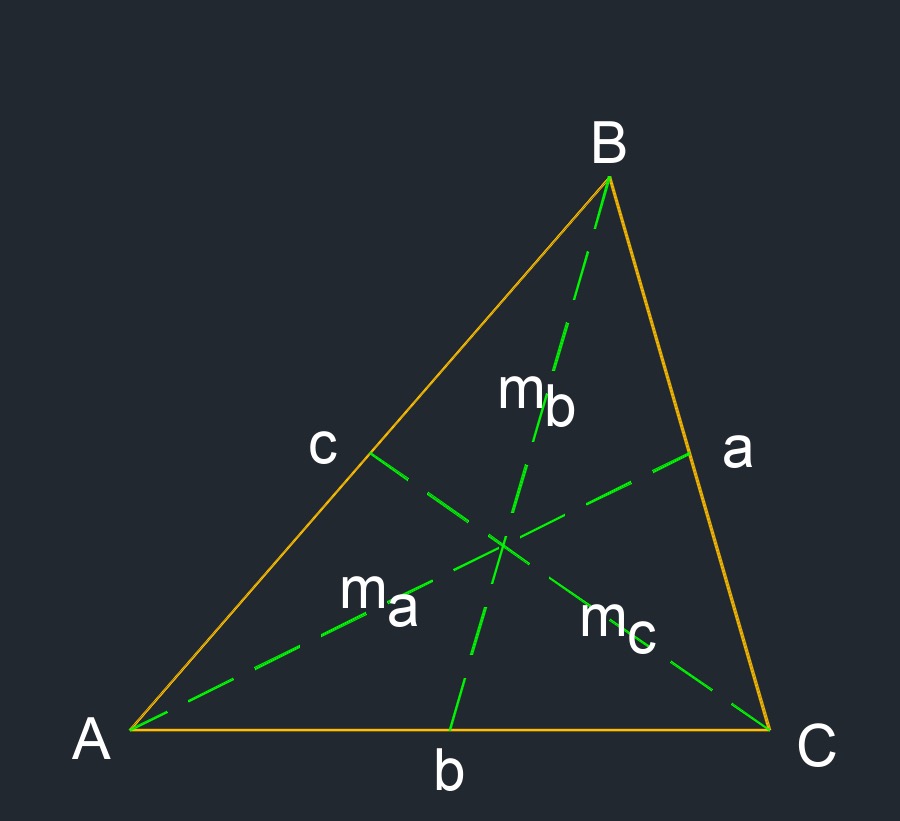
Median of a scalene triangle is a line segment from a vertex (coiner point) to the midpoint of the opposite side.
Circumcircle is a circle that passes through all the vertices of a two-dimensional figure.
Inscribed circle is the Iargest circle possible that can fit on the inside of a two-dimensional figure.
Semiperimeter is one half of the perimeter.
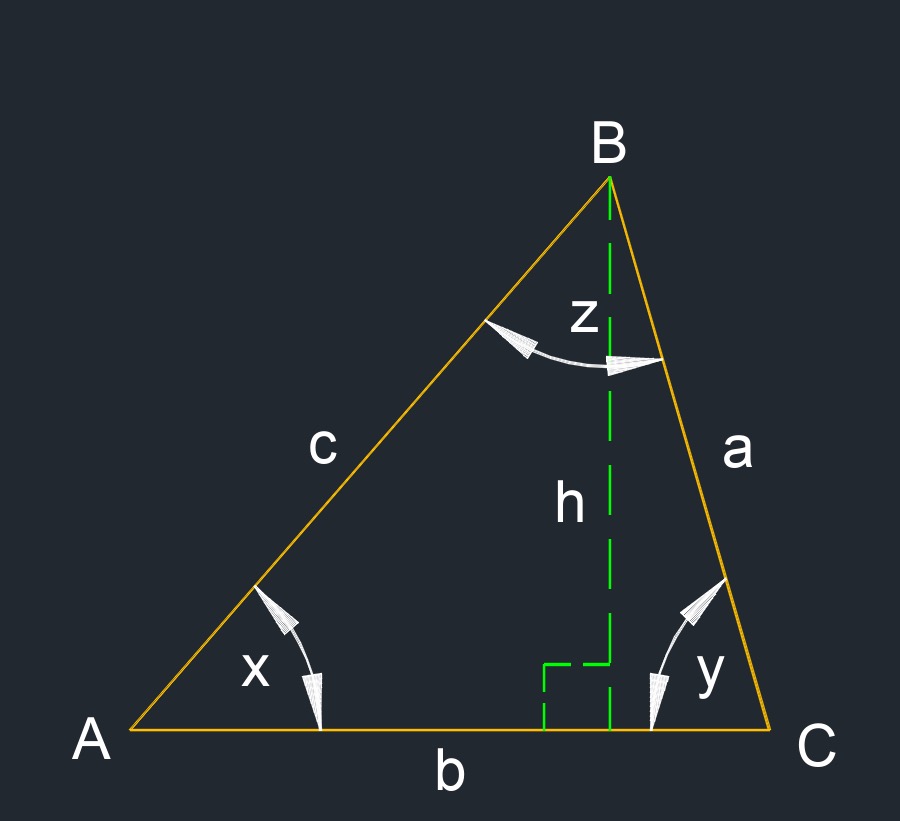
x + y + z = 180°
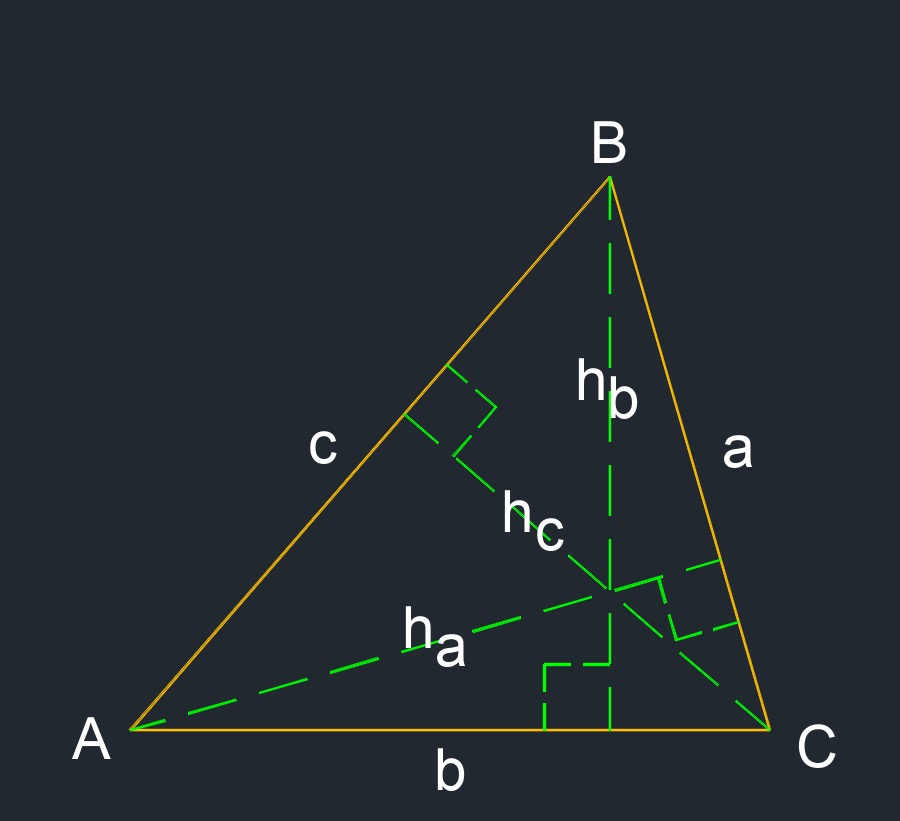
Height: \(h_a\), \(h_b\), \(h_c\)
Median: \(m_a\), \(m_b\), \(m_c\) - A line segment from a vertex (corner point) to the midpoint of the opposite side
Angle bisectors: \(t_a\), \(t_b\), \(t_c\) - A line that splits an angle into two equal angles
3 edges
3 vertexs

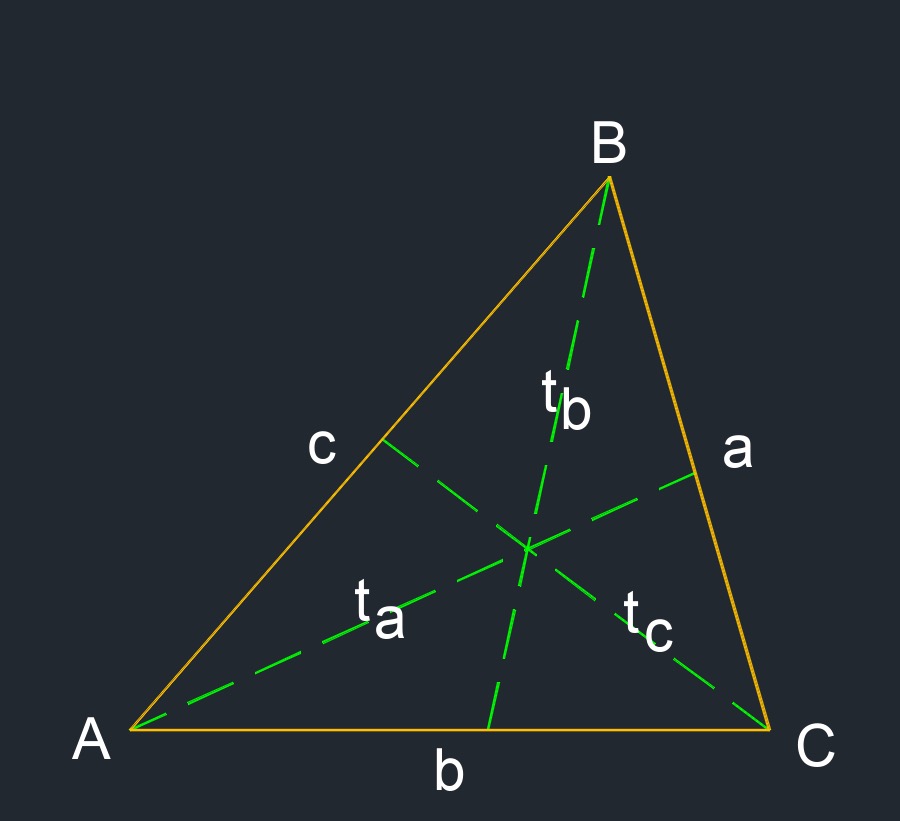
scalene triangle 5h scalene triangle 5m scalene triangle 5t

Angle bisector of a Scalene Triangle formulas
\(\large{ t_a = 2\;b \;c \; cos \; \frac { \frac {A}{2} } { b \;+\; c } }\) \(\large{ t_a = \sqrt { b\;c \; \frac { 1 \;- \; a^2 }{ \left( b \;+\; c \right)^2 } } }\)
Symbol	English	Metric
\(\large{ t_a }\) = angle bisector	\(\large{ in}\)	\(\large{ mm }\)
\(\large{ \theta }\) = angle	\(\large{deg}\)	\(\large{rad}\)
\(\large{ a, b, c }\) = edge	\(\large{ in}\)	\(\large{ mm }\)

Area of a Scalene Triangle formulas
\(\large{ A_{area} = \frac {h\;b} {2} }\) \(\large{ A_{area} = a\;b\; \frac {\sin y} {2} }\)
Symbol	English	Metric
\(\large{ A_{area} }\) = area	\(\large{ in^2}\)	\(\large{ mm^2}\)
\(\large{ a, b, c }\) = edge	\(\large{ in}\)	\(\large{ mm }\)

Circumcircle of a Scalene Triangle formulas
\(\large{ R = \sqrt { \frac { a^2 \; b^2 \; c^2 } { \left( a \;+\; b \;+\; c \right) \; \left( - a + b + c \right) \; \left( a \;-\; b \;+\; c \right) \; \left( a \;+\; b \;-\; c \right) } } }\) \(\large{ R = \frac { a \; b \; c } { 4 \; \sqrt { s\; \left( s \;-\; a \right) \; \left( s \;-\; b \right) \; \left( s \;-\; c \right) } } }\)
Symbol	English	Metric
\(\large{ R }\) = outcircle	\(\large{ in}\)	\(\large{ mm }\)
\(\large{ a, b, c }\) = edge	\(\large{ in}\)	\(\large{ mm }\)
\(\large{ s }\) = semiperimeter	\(\large{ in}\)	\(\large{ mm }\)

Height of a Scalene Triangle formulas
\(\large{ h_a = c \; sin\; B }\) \(\large{ h_a = b \; sin\; C }\) \(\large{ h_a = 2\; \frac {A_{area}}{a} }\)
Symbol	English	Metric
\(\large{ h_a }\) = height	\(\large{ in}\)	\(\large{ mm}\)
\(\large{ B, C }\) = angle	\(\large{ deg}\)	\(\large{ rad}\)
\(\large{ A_{area} }\) = area	\(\large{ in^2}\)	\(\large{ mm^2 }\)
\(\large{ a, b, c }\) = edge	\(\large{ in}\)	\(\large{ mm }\)

Inscribed Circle of a Scalene Triangle formula
\(\large{ r = \sqrt { \frac { \left( s \;-\; a \right) \; \left( s \;-\; b \right) \; \left( s \;-\; c \right) } { s } } }\)
Symbol	English	Metric
\(\large{ r }\) = incircle	\(\large{ in}\)	\(\large{ mm }\)
\(\large{ a, b, c }\) = edge	\(\large{ in}\)	\(\large{ mm }\)

Median of a Scalene Triangle formula
\(\large{ m_a = \sqrt { \frac { 2\;b^2 \;+\; 2\;c^2 \;-\; a^2 } {2} } }\)
Symbol	English	Metric
\(\large{ m_a }\) = median	\(\large{ in}\)	\(\large{ mm }\)
\(\large{ a, b, c }\) = edge	\(\large{ in}\)	\(\large{ mm }\)

Perimeter of a Scalene Triangle formula
\(\large{ P = a + b + c }\)
Symbol	English	Metric
\(\large{ P }\) = perimeter	\(\large{ in}\)	\(\large{ mm }\)
\(\large{ a, b, c }\) = edge	\(\large{ in}\)	\(\large{ mm }\)

Semiperimeter of a Scalene Triangle formula
\(\large{ s = \frac{ a \;+\; b \;+\; c }{ 2 } }\)
Symbol	English	Metric
\(\large{ s }\) = semiperimeter	\(\large{ in}\)	\(\large{ mm }\)
\(\large{ a, b, c }\) = edge	\(\large{ in}\)	\(\large{ mm }\)

Side of a Scalene Triangle formulas
\(\large{ a = P - b - c }\) \(\large{ a = 2\; \frac {A_{area}} {b\;\sin y} }\) \(\large{ b = P - a - c }\) \(\large{ b = 2\; \frac {A_{area}}{h} }\) \(\large{ c = P - a - b }\)
Symbol	English	Metric
\(\large{ a, b, c }\) = edge	\(\large{ in}\)	\(\large{ mm }\)
\(\large{ A_{area} }\) = area	\(\large{ in^2}\)	\(\large{ mm^2 }\)
\(\large{ P }\) = perimeter	\(\large{ in}\)	\(\large{ mm }\)

Trig Functions
Find A given a c : \(\; sin \; A= a \div c \) given b c : \(\; cos \; A= b \div c \) given a b : \(\; tan \; A= a \div b \)
Find B given a c : \(\; sin \; B= a \div c \) given b c : \(\; cos \; B= b \div c \) given a b : \(\; tan \; B= b \div a \)
Find a given A c : \(\; a= csin \; A \) given A b : \(\; a= btan \; A \)
Find b given A c : \(\; b= c*cos \; A \) given A a : \(\; b= a \div tan \; A \)
Find c given A a : \(\; c= a \div sin \; A \) given A b : \(\; c= b \div cos \; A \) given a b : \(\; c= \sqrt { a^2+b^2 } \)
Find Area given a b : \(\; Area= a\;b \div 2 \)

Piping Designer Logo 1

Angle bisector of a Scalene Triangle formulas