Regular Pentagon

on 29 January 2016. Posted in Plane Geometry

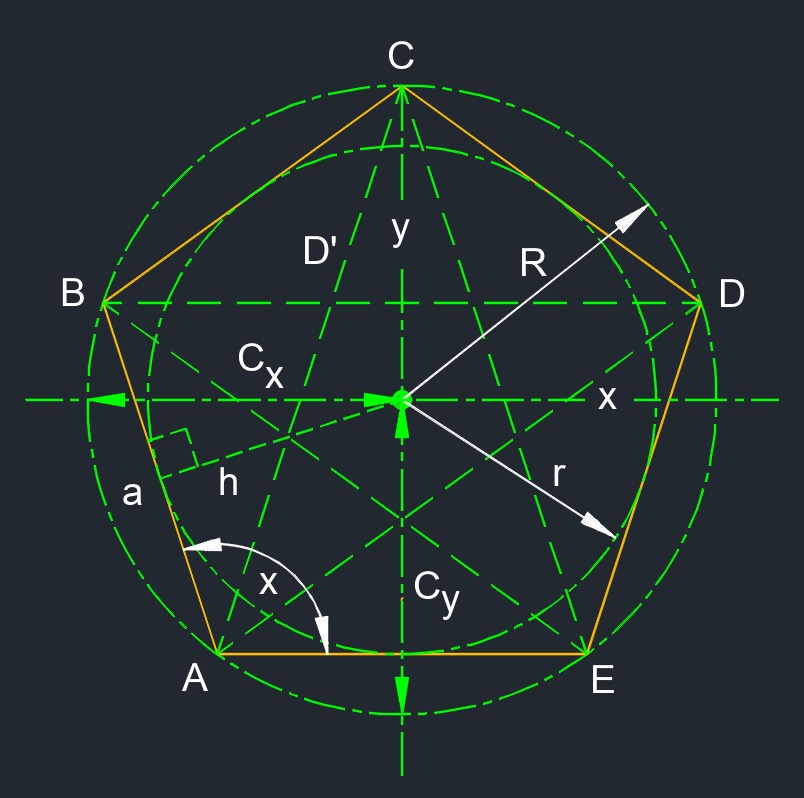Regular pentagon (a two-dimensional figure) is a polygon with five congruent sides.
Circumcircle is a circle that passes through all the vertices of a two-dimensional figure.
Congruent is all sides having the same lengths and angles measure the same.
Diagonal is a line from one vertices to another that is non adjacent.
Inscribed circle is the largest circle possible that can fit on the inside of a two-dimensional figure.
Polygon (a two-dimensional figure) is a closed plane figure for which all edges are line segments and not necessarly congruent.
Exterior angles are 72°.
Interior angles are 108°.
3 triangles created from any one vertex.
Diagonals do not cross the center point of the pentagon.
5 diagonals
5 edges
5 vertexs

Area of a Regular Pentagon formula
\(\large{ A_{area} = \frac {a\;r}{2} }\)
Symbol	English	Metric
\(\large{ A_{area} }\) = area	\(\large{ in^2 }\)	\(\large{ mm^2 }\)
\(\large{ a }\) = edge	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ r }\) = inside radius	\(\large{ in }\)	\(\large{ mm }\)

Circumcircle Radius of a Regular Pentagon formula
\(\large{ R = \frac{a}{2} \; csc \; \frac{180°}{n} }\)
Symbol	English	Metric
\(\large{ R }\) = outside radius	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ a }\) = edge	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ n }\) = number of edges	\(\large{ dimensionless }\)

Diagonal of a Regular Pentagon formula
\(\large{ D' = \frac{ 1 \;+\; \sqrt { 5} }{2} \; a }\)
Symbol	English	Metric
\(\large{ D' }\) = diagonal	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ a }\) = edge	\(\large{ in }\)	\(\large{ mm }\)

Edge of a Regular Pentagon formulas
\(\large{ a = 25^{3/4}\; \frac { \sqrt{A_{area}} } { 5\; \left( \sqrt {20} \;+\; 5 \right) ^{1/4 } } }\) \(\large{ a = D' \;\frac { -1 \;+\; \sqrt { 5} } {2} }\)
Symbol	English	Metric
\(\large{ a }\) = edge	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ A_{area} }\) = area	\(\large{ in^2 }\)	\(\large{ mm^2 }\)
\(\large{ D' }\) = diagonal	\(\large{ in }\)	\(\large{ mm }\)

Inscribed Circle Radius of a Regular Pentagon formula
\(\large{ r = \frac{a}{2} \; cot \; \frac{180°}{n} }\)
Symbol	English	Metric
\(\large{ R }\) = outside radius	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ a }\) = edge	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ n }\) = number of edges	\(\large{ dimensionless }\)

Perimeter of a Regular Pentagon formula
\(\large{ p= 5 \;a }\)
Symbol	English	Metric
\(\large{ p }\) = perimeter	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ a }\) = edge	\(\large{ in }\)	\(\large{ mm }\)

Piping Designer Logo 1

Area of a Regular Pentagon formula