Regular Hexagon
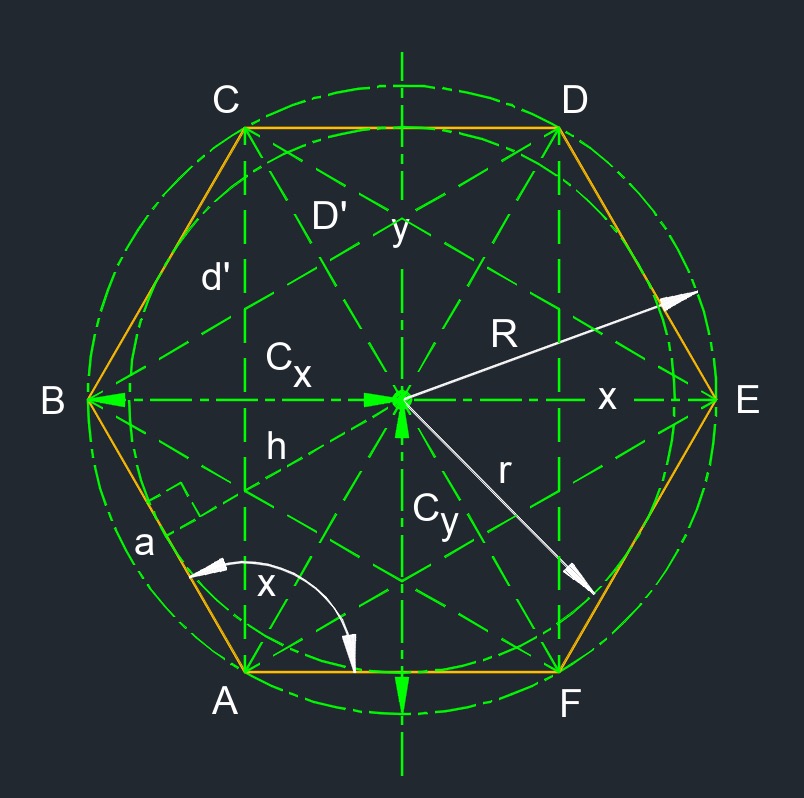 Regular hexagon (a two-dimensional figure) is a polygon with six congruent sides.
Regular hexagon (a two-dimensional figure) is a polygon with six congruent sides.- Circumcircle is a circle that passes through all the vertices of a two-dimensional figure.
- Congruent is all sides having the same lengths and angles measure the same.
- Diagonal is a line from one vertices to another that is non adjacent.
- Inscribed circle is the largest circle possible that can fit on the inside of a two-dimensional figure.
- Long diagonal always crosses the center point of the hexagon.
- Polygon (a two-dimensional figure) is a closed plane figure for which all edges are line segments and not necessarly congruent.
- Short diagonal does not cross the center point of the hexagon.
- Exterior angles are 60°.
- Interior angles are 120°.
- 9 diagonals
- 6 edges
- 6 vertexs
Regular Hexagon Index
- Area of a Regular Hexagon
- Circumcircle Radius of a Regular Hexagon
- Edge of a Regular Hexagon
- Inscribed Circle Radius of a Regular Hexagon
- Perimeter of a Regular Hexagon
- Long Diagonal of a Regular Hexagon
- Short Diagonal of a Regular Hexagon
Area of a Regular Hexagon formula |
||
| \(\large{ A_{area} = \frac {3}{2} \; \sqrt{3} \; a^2 }\) | ||
| Symbol | English | Metric |
| \(\large{ A_{area} }\) = area | \(\large{ in^2 }\) | \(\large{ mm^2 }\) |
| \(\large{ a }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
Circumcircle Radius of a Regular Hexagon formula |
||
| \(\large{ R = a }\) | ||
| Symbol | English | Metric |
| \(\large{ R }\) = circumcircle radius | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
Edge of a Regular Hexagon formulas |
||
|
\(\large{ a = \frac { p } {6} }\) \(\large{ a = 3^{1/4}\; \sqrt { 2\; \frac {A_{area}}{9} } }\) |
||
| Symbol | English | Metric |
| \(\large{ a }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ A_{area} }\) = area | \(\large{ in^2 }\) | \(\large{ mm^2 }\) |
| \(\large{ p }\) = perimeter | \(\large{ in }\) | \(\large{ mm }\) |
Inscribed Circle Radius of a Regular Hexagon formula |
||
| \(\large{ r = \frac{ \sqrt{3} }{2} \; a }\) | ||
| Symbol | English | Metric |
| \(\large{ r }\) = inside radius | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
Perimeter of a Regular Hexagon formula |
||
| \(\large{ p = 6 \;a }\) | ||
| Symbol | English | Metric |
| \(\large{ p }\) = perimeter | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
Long Diagonal of a Regular Hexagon formula |
||
| \(\large{ D' = 2 \;a }\) | ||
| Symbol | English | Metric |
| \(\large{ D' }\) = long diagonal | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
Short Diagonal of a Regular Hexagon formula |
||
| \(\large{ d' = \sqrt{3}\;a }\) | ||
| Symbol | English | Metric |
| \(\large{ d' }\) = short diagonal | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |

