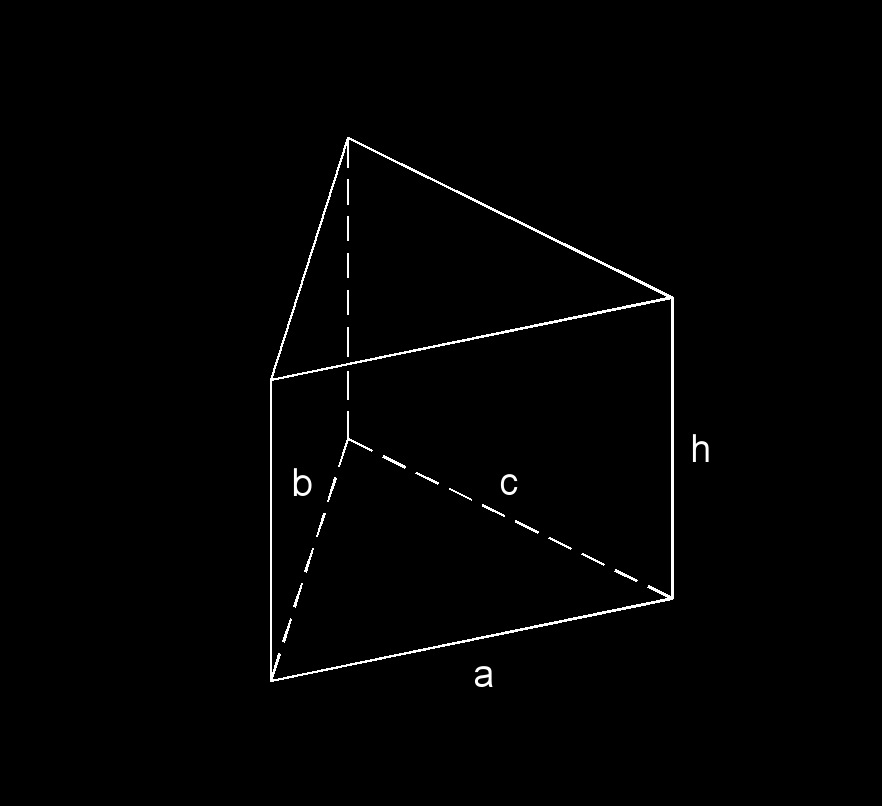
Triangular Prism

 Edge formula
Edge formula
\(a = \frac {A_l } {h} - b-c \)
\(b = \frac {A_l } {h} - a-c \)
\(c = \frac {A_l } {h} - a-b \)
Where:
\(a\) = edge
\(b\) = edge
\(c\) = edge
\(h\) = height
\(A_l\) = lateral surface area
Height formula
\(h = \frac {A_l } {a+b+c } \)
Where:
\(h\) = height
\(A_l\) = lateral surface area
\(a\) = edge
\(b\) = edge
\(c\) = edge
Base Area formula
\(A_b = \frac {1}{4} \sqrt { -b^4 + 2 \left( b c \right)^2 +2 \left( b a \right)^2 -c^4 +2 \left( c a \right)^2 -a^4 } \)
Where:
\(A_b\) = base area
\(a\) = edge
\(b\) = edge
\(c\) = edge
Lateral Surface Area formula
\(A_l = \left( a+b+c \right) h \)
Where:
\(A_l\) = lateral surface area
\(a\) = edge
\(b\) = edge
\(c\) = edge
\(h\) = height
Volume formula
\(V = \frac {1}{4} h \sqrt { -b^4 + 2 \left( b c \right)^2 +2 \left( b a \right)^2 -c^4 +2 \left( c a \right)^2 -a^4 } \)
Where:
\(V\) = volume
\(a\) = edge
\(b\) = edge
\(c\) = edge
\(h\) = height
