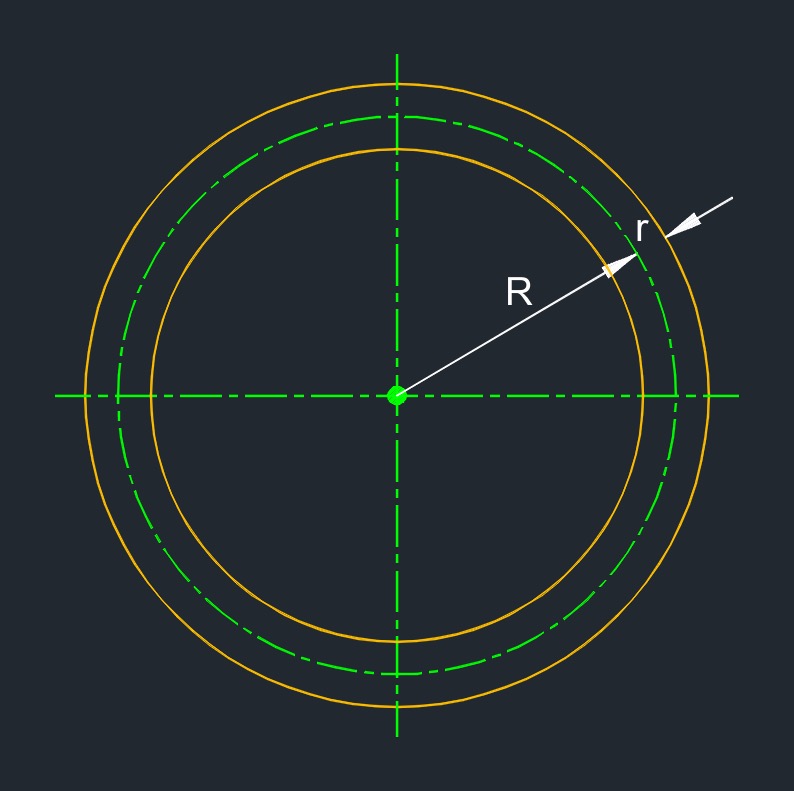
Torus
A three-dimensional figure shaped like a donut.
Hole Radius of a torus formula
\(\large{ R_h = R - r }\)
Where:
\(\large{ R_h }\) = radius of the hole
\(\large{ r }\) = radius of sphere
\(\large{ R }\) = radius of center of sphere
Surface Area of a torus formula
\(\large{ S = 4 \; \pi^2 \; R\; r }\)
Where:
\(\large{ S }\) = surface area
\(\large{ \pi }\) = Pi
\(\large{ r }\) = radius of sphere
\(\large{ R }\) = radius of center of sphere
Volume of a torus formula
\(\large{ V = 2 \; \pi^2 \; R\; r^2 }\)
Where:
\(\large{ V }\) = volume
\(\large{ \pi }\) = Pi
\(\large{ r }\) = radius of sphere
\(\large{ R }\) = radius of center of sphere