Force
Force Formula |
||
|
\( F \;=\; m \cdot a \) (Force) \( m \;=\; \dfrac{ F }{ a } \) \( a \;=\; \dfrac{ F }{ m } \) |
||
| Symbol | English | Metric |
| \( F \) = Force | \(lbf\) | \(N\) |
| \( m \) = Mass | \(lbm\) | \(kg\) |
| \( a \) = Acceleration | \(ft \;/\; sec^2\) | \(m \;/\; s^2\) |
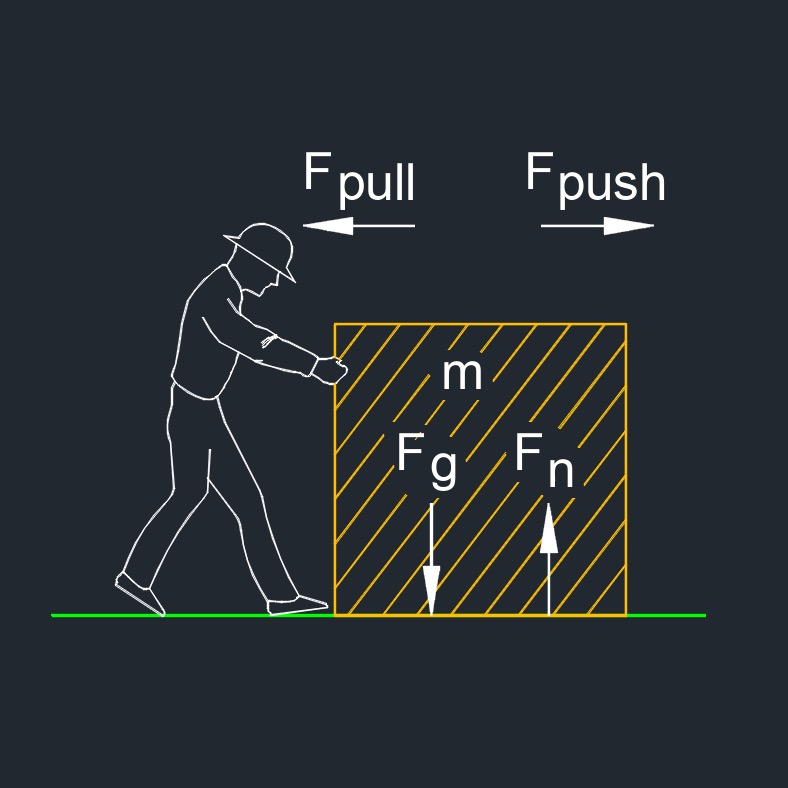 Force, abbreviated as F, is a physical quantity that represents a push or pull applied to an object, resulting in its motion, deformation, or change in velocity. In simpler terms, force is what causes objects to accelerate or change their state of motion. It is a fundamental concept in physics and is described by Sir Isaac Newton's second law of motion. So when you apply force to an object the velocity changes, the change in velocity is acceleration. Force is a vector quantity having both magnitude and direction.
Force, abbreviated as F, is a physical quantity that represents a push or pull applied to an object, resulting in its motion, deformation, or change in velocity. In simpler terms, force is what causes objects to accelerate or change their state of motion. It is a fundamental concept in physics and is described by Sir Isaac Newton's second law of motion. So when you apply force to an object the velocity changes, the change in velocity is acceleration. Force is a vector quantity having both magnitude and direction.
Force Units | |||||
|---|---|---|---|---|---|
| newton | dyne | kilogram-force, kilopond | pound-force | poundal | |
| \(1\;N\) | \(\equiv \; 1\; kg \cdot m/s^2\) | \(=\; 10^5 \;dyn\) | \(\approx\; 0.10197 \;kp\) | \(\approx\; 0.22481 \;lb_F\) | \(\approx\; 7.2330 \;pdl\) |
| \(1\;dyn\) | \(= \;10^{-5} N\) | \(\equiv\; 1 \; g \cdot cm/s^2 \) | \(\approx\; 1.0197 x 10^{-6} \;kp\) | \(\approx\; 2.2481 x 10^{-6} \;lb_F\) | \(\approx\; 7.2330 x 10^{-5}\;pdl\) |
| \(1\;kp\) | \(= \;9.80665 \;N\) | \(=\; 980665 \;dyn\) | \(\equiv \; g_n \cdot 1\;kg\) | \(\approx\; 2.2046 \;lb_F\) | \(\approx\; 70.932 \;pdl\) |
| \(1\;lb_F\) | \(\approx\; 4.448222 \;N\) | \(\approx\; 444822 \;dyn\) | \(\approx\; 0.45359 \;kp\) | \(\equiv \; g_n \cdot 1\;lb\) | \(\approx\; 32.174 \;pdl\) |
| \(1\;pdl\) | \(\approx\; 0.138255 \;N\) | \(\approx\; 13825 \;dyn\) | \(\approx\; 0.014098 \;kp\) | \(\approx\; 0.031081 \;lb_F\) | \(\equiv \; 1\; lb \cdot ft/s^2\) |
| The value of gn (9.80665 m/s2) as used in the official definition of the kilogram-force is used here for all gravitational units. | |||||
Force Index
All forces can be divided into two basic types of forces:
Contact Force - Contact forces are those forces that arise when two objects physically touch each other. These are some of the main types of contact forces. Each of these forces has its own unique characteristics and effects on objects in contact. Here are some types of contact forces:
- Air Resistance or Drag Force - This force opposes the motion of an object through a fluid (usually air). It becomes significant at higher speeds and can affect the motion of objects like vehicles, projectiles, and falling objects.
- Applied Force - This is a force that is applied directly to an object by a person, another object, or a machine. For example, when you push a box across the floor, you're applying an applied force.
- Buoyant Force - This force is exerted by a fluid (liquid or gas) on an object immersed in it. It opposes the force of gravity and is what allows objects to float in liquids.
- Compression Force - Compression is the force that occurs when an object is compressed or pushed together. It's the opposite of tension and is observed, for instance, when you press down on a spring.
- Elastic Force - This force arises when an object is deformed (stretched or compressed) and then returns to its original shape when the deforming force is removed. Examples include a stretched rubber band or a compressed spring.
- Frictional Force - Friction is the force that opposes the relative motion or tendency of motion between two surfaces in contact. There are two main types of friction:
- Static Friction - This is the friction that prevents an object from starting to move relative to a surface. It's the force that must be overcome to initiate motion.
- Kinetic Friction - Also known as sliding friction, this is the friction that opposes the motion of an object already in motion across a surface.
- Muscular Force - Muscles work together to create a force that is known as muscular force. Muscle force only occurs when it comes into touch with anything.
- Normal Force - This is the force exerted by a surface that supports an object's weight. For example, when you place a book on a table, the table exerts an upward force on the book to counteract its weight due to gravity.
- Shear Force - Shear forces occur when two objects slide past each other in opposite directions. This is common in materials like fluids and in certain types of structures.
- Spring Force - The force that compresses (a repulsive force) or stretches (an attractive force) the spring.
- Tension Force - Tension is the force that occurs when an object is pulled or stretched by a force acting along its length. This is commonly observed in things like ropes, cables, and strings.
Non-contact Force - Non-contact forces are forces that act on objects without any physical contact between the objects themselves. These forces can affect objects from a distance. These non-contact forces play a crucial role in the behavior of the universe at various scales, from the subatomic to the cosmic level. Here are some types of non-contact forces:
- Casimir Force - This is a quantum mechanical force that arises between two closely spaced uncharged conductive surfaces due to the vacuum fluctuations of the electromagnetic field.
- Electromagnetic Force - This force includes several subtypes:
- Electric Force - The force that arises due to the presence of electric charges. Like charges repel each other, and opposite charges attract.
- Magnetic Force - The force exerted by magnets or moving charges on other magnets or charges. It's responsible for phenomena like magnetism and the behavior of compass needles.
- Electrostatic Force - This is the force of attraction or repulsion between stationary electric charges. It's a specific type of electromagnetic force that occurs when charges are not in motion.
- Gravitational Force - This is the force of attraction between any two masses in the universe. It's what keeps planets in orbit around the Sun, and it's responsible for the weight of objects on the surface of the Earth.
- Gravity Wave - These are ripples in spacetime caused by the acceleration of massive objects, according to Einstein's theory of general relativity. Gravity waves were first directly observed in 2015 and provide insight into astronomical events like merging black holes.
- Lorentz Force - This force acts on a charged particle moving through an electromagnetic field. It's the combined effect of electric and magnetic forces on a moving charge.
- Magnetic Force - As mentioned earlier, this force is exerted by magnets or moving charges. It's responsible for various magnetic effects, such as the behavior of compasses and the operation of many electrical devices.
- Nuclear Force - These are the forces that hold the nucleus of an atom together. They include the strong nuclear force, which binds protons and neutrons together, and the weak nuclear force, which is involved in certain types of radioactive decay.
- Van der Waals Force - This force is a type of weak attraction that exists between molecules or atoms, even if they are not charged. It arises due to temporary fluctuations in electron distribution, leading to temporary dipoles in neighboring particles.
Three-dimensional forces the are forces that act in three-dimensional space, which means they have components in three perpendicular directions: X-axis, Y-axis, and Z-axis. These forces are commonly encountered in physics and engineering, where objects and systems can experience forces from multiple directions. In three-dimensional forces, each force vector can be decomposed into three components along the three axes. The vector sum of these components represents the overall force acting on an object.
For example, if F is a three-dimensional force vector, its components along the X, Y, and Z axes can be represented as Fx, Fy, and Fz, respectively. The complete force vector F is then the sum of these three components:
F = Fxi + Fyj + Fzk
Here, i, j, and k are the unit vectors along the X, Y, and Z axes, respectively.
Understanding three-dimensional forces is crucial in analyzing the motion and equilibrium of objects in three-dimensional space, especially in fields such as mechanics, physics, and engineering.
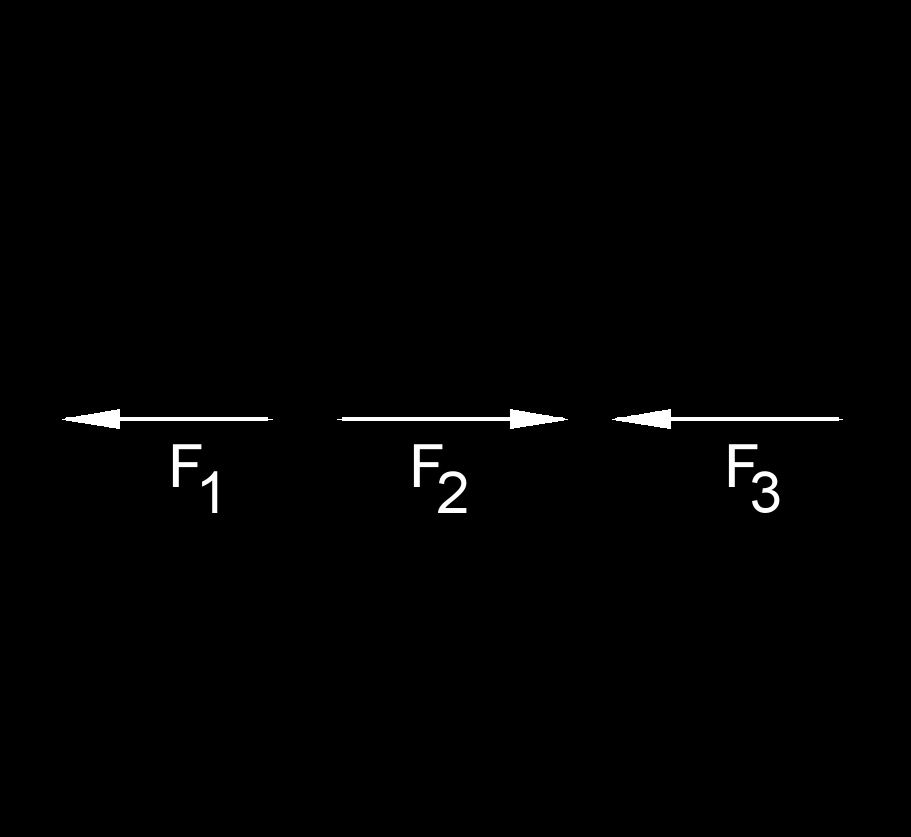 Collinear Force - All share the same line of action.
Collinear Force - All share the same line of action.
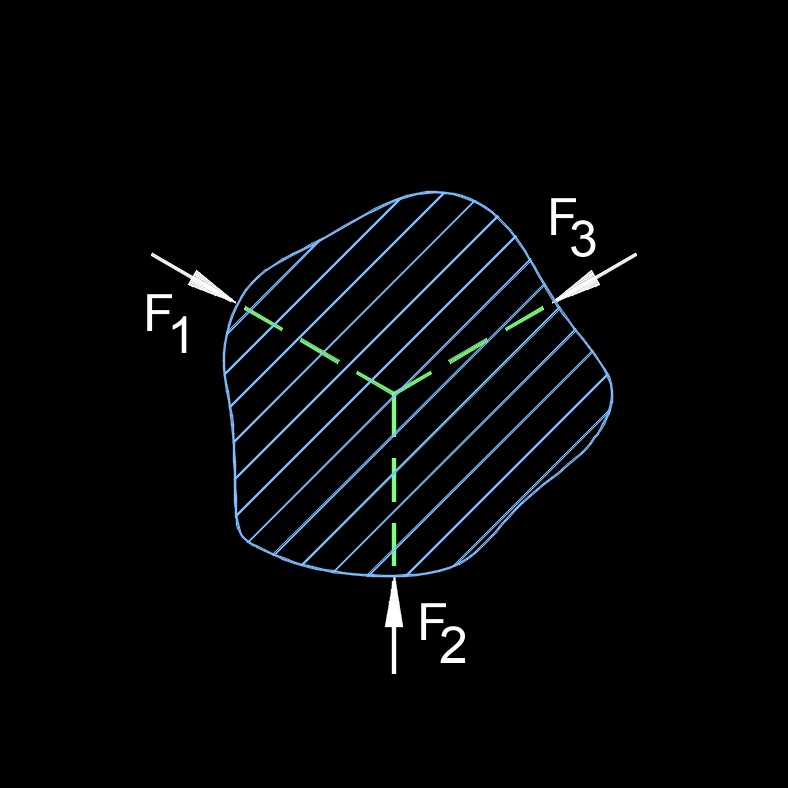 Concurrent Force - All acting at the same point.
Concurrent Force - All acting at the same point.
 Coplannar Parallel Force - Can be in the same or opposite direction and are on the same plane.
Coplannar Parallel Force - Can be in the same or opposite direction and are on the same plane.
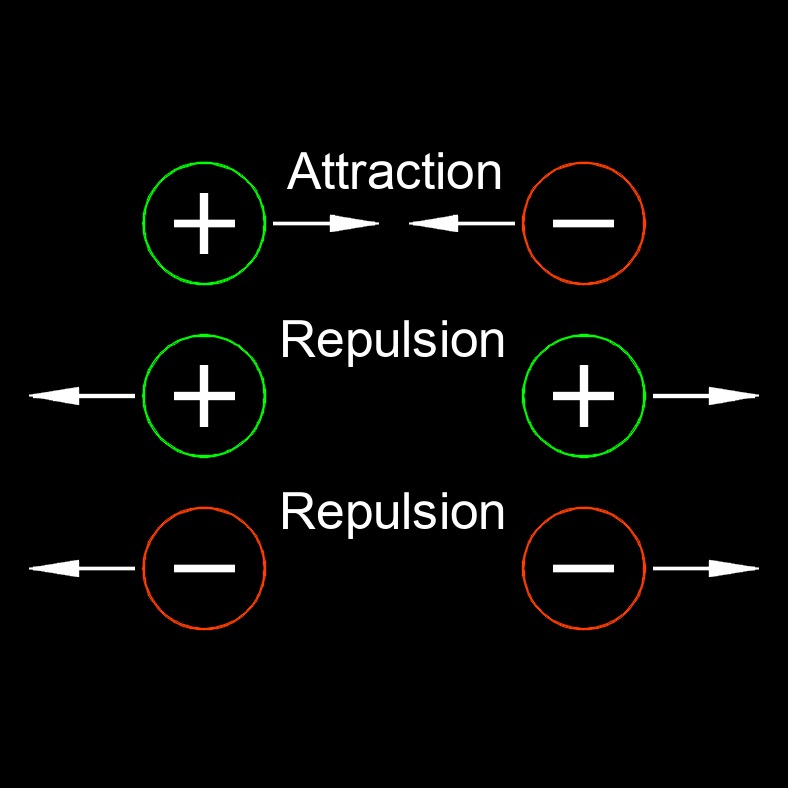 Electric Force - An attraction or repulsion force between any two charged objects.
Electric Force - An attraction or repulsion force between any two charged objects.
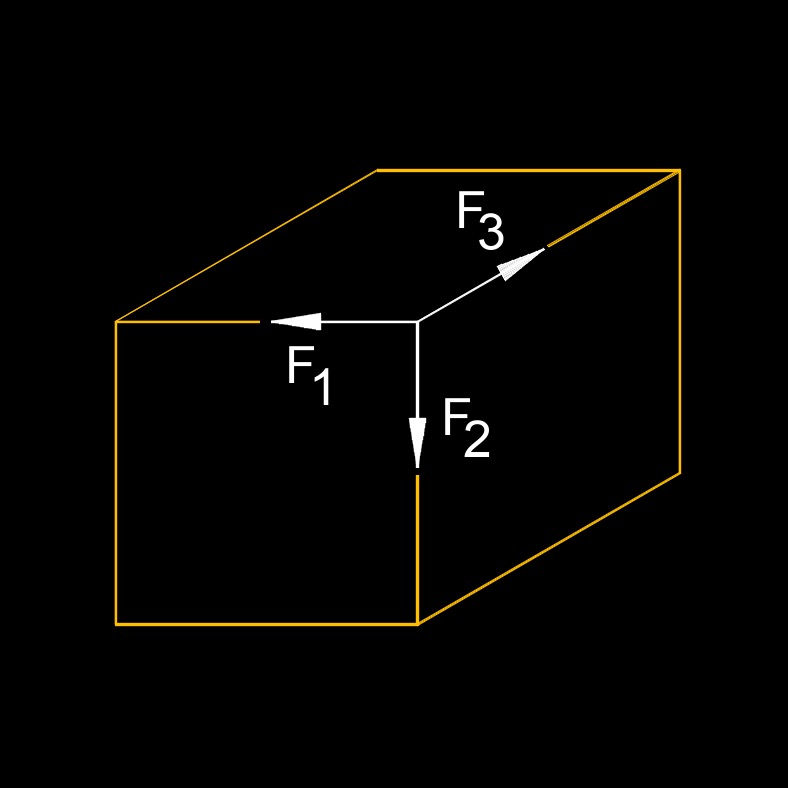 Non-coplannar Concurrent Force - Act at the same point but their lines of action lie on different planes.
Non-coplannar Concurrent Force - Act at the same point but their lines of action lie on different planes.


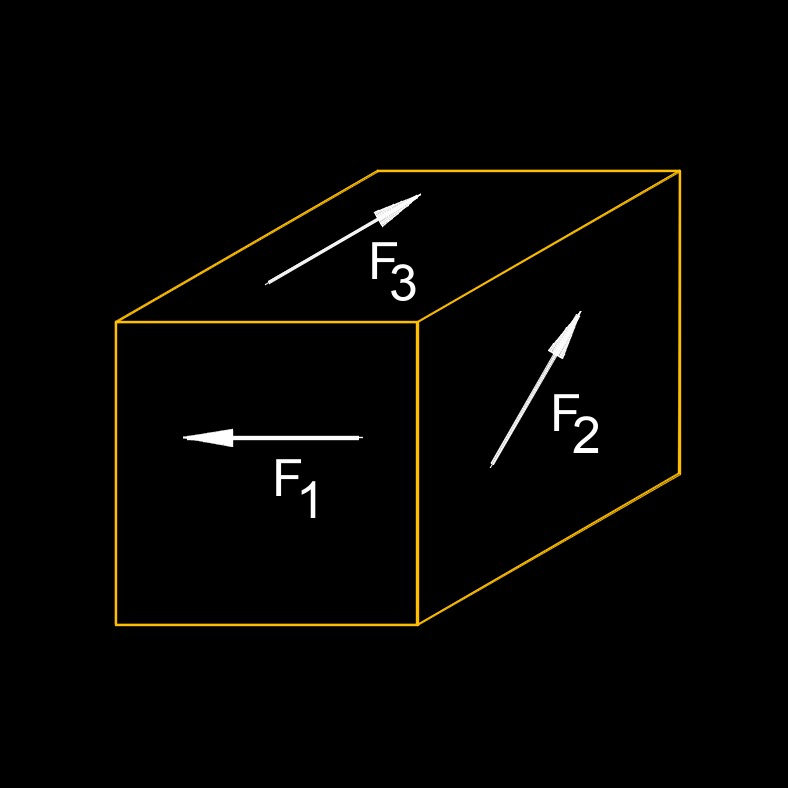 Non-coplannar Force
Non-coplannar Force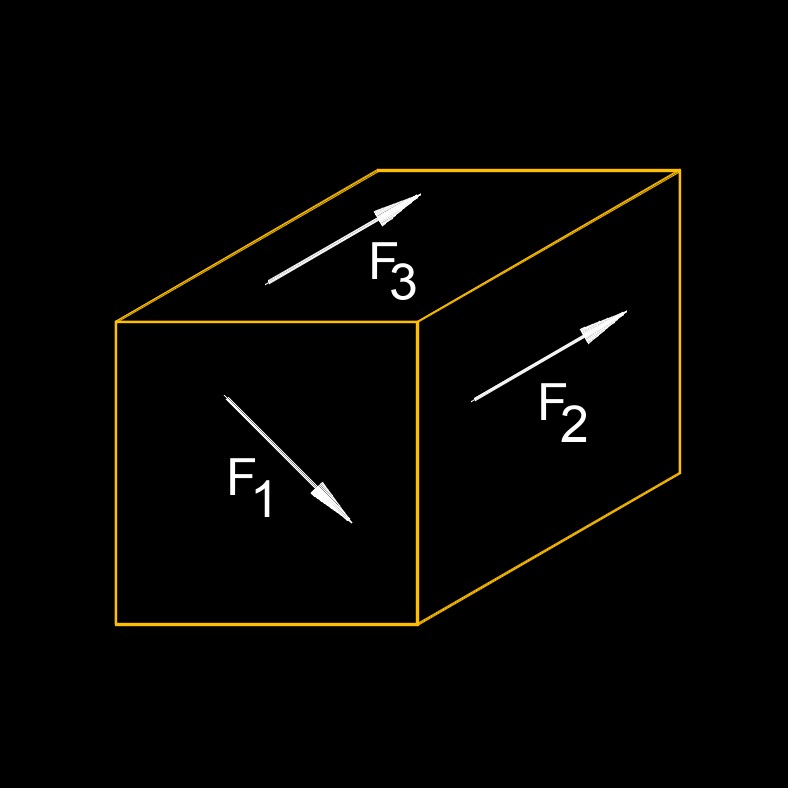 Non-coplannar Non-concurrent Force
Non-coplannar Non-concurrent Force