Skip to main content

Projectile Launch Angle

  

Projectile Launch Angle formula

  • Horizontal  -  \(v_x \;=\; v_o \cdot cos(\theta)\), determines how far the projectile travels.
  • Vertical  -  \(v_y \;=\; v_o \cdot sin(\theta)\), determines how high it goes and how long it stays in the air.  Here, \(v_o\), is the initial speed of the projectile.
\(  \theta \;=\; \dfrac{  v_o^2 \cdot  sin(2\theta)   }{  g  } \) 
Symbol English Metric
\( \theta \) = Angle of the Initial Vertical from x-axis \( deg \) \( rad \)
\( v_o \) = Initial Speed of the Projectile \(ft\;/\;sec\)  \(m\;/\;s\) 
\( g \) = Gravitational Acceleration  \(ft\;/\;sec^2\)   \(m\;/\;s^2\)   
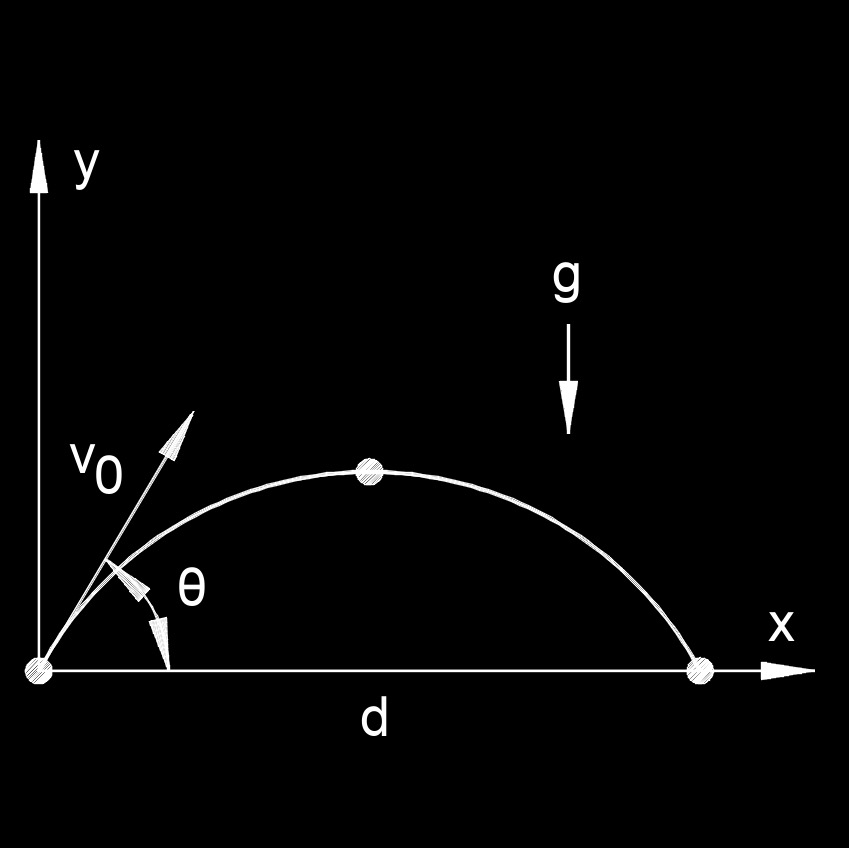trajectory angle 1Projectile launch angle is the angle at which an object (a projectile) is launched relative to a reference direction, usually the horizontal plane, when it’s set into motion under the influence of gravity (and typically no other forces like air resistance, unless specified).  It’s a critical factor in determining the trajectory, range, and height of the projectile’s path.
 
  • The horizontal distance the projectile travels is maximized at a launch angle of \(45^{\circ}\) (assuming no air resistance and a flat surface), because this balances the horizontal and vertical components optimally.
  • A steeper angle (closer to \(90^{\circ}\)) sends the projectile higher but reduces its range.
  • The time in the air increases with a higher angle up to \(90^{\circ}\), where it’s longest (but range drops to zero since it goes straight up and down).
  • In real life, like with cannons, basketball shots, or spacecraft, air resistance and other factors tweak this, but the launch angle is still the starting point for predicting the path.

Piping Designer Logo 1