Moment of Inertia

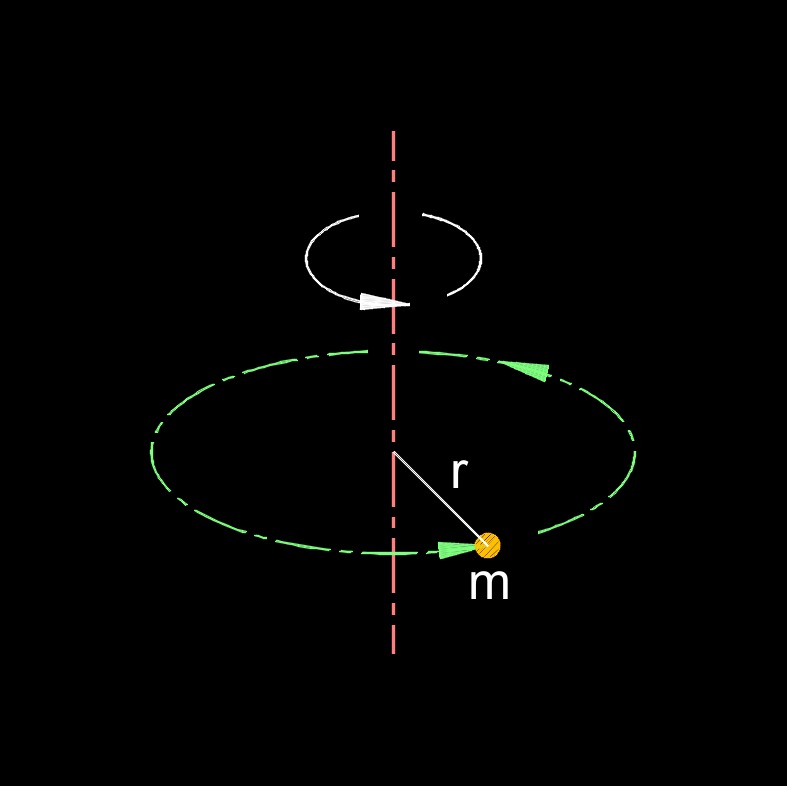Moment of inertia, abbreviated as I, also called rotational inertia, measures the resists or change an object has to rotational acceleration about an axis.  It is analogous to the mass of an object in linear motion and plays a similar role in rotational dynamics.  The larger the moment of inretia the more difficult to try to get an object moving and the smaller the moment of inretia the easier of relatively easier to get an object moving.

The moment of inertia depends on the distribution of mass around the axis of rotation.  Objects with more mass concentrated farther from the axis of rotation have larger moments of inertia, while objects with mass distributed closer to the axis have smaller moments of inertia.

The moment of inertia varies depending on the shape and size of the object.  For simple geometric shapes, such as cylinders, spheres, or rectangular solids, there are specific formulas to calculate their moments of inertia.  For more complex objects, the moment of inertia can be found by integration, summing infinitesimally small mass elements throughout the object.  Moment of inertia is a fundamental concept in rotational dynamics and provides insights into how objects rotate and respond to external torques.

Inertia is the tendency of an object in motion to remain in motion or an object at rest to remain at rest unless acted upon by a force.  The larger the mass of an object the more resistance to change in motion than objects of a lesser mass.  It is the tendency of objects to keep moving in a straight line at a constant velocity and direction forever unless acted upon by gravity or another force.

First Moment of Area  -  Abbreviated as Q, also called first moment of inertia, (English mass unit \(\large{\frac{lbm}{ft^2-sec} }\), Metric mass unit \(\large{\frac{kg}{m^2} }\)), is the measurement of a shape's area cross-section relative to an axis, located in space.  In practical terms and of relavance to this site, the shape is generally a beam or piece of pipe.  It is the resistance of an object to bend around a certain axis.  It can be used to determine the location of the centroid, which is the point where the sum of all moments of inertia are equal.

Second Moment of Area  -  Abbreviated as I, also called second area moment or area moment of inertia, (English area unit \(in^4\), Metric area unit \(mm^4\)), is the resistance of an object to bend around a certain axis of a area cross-section.  This is used in engineering of beams and supports.