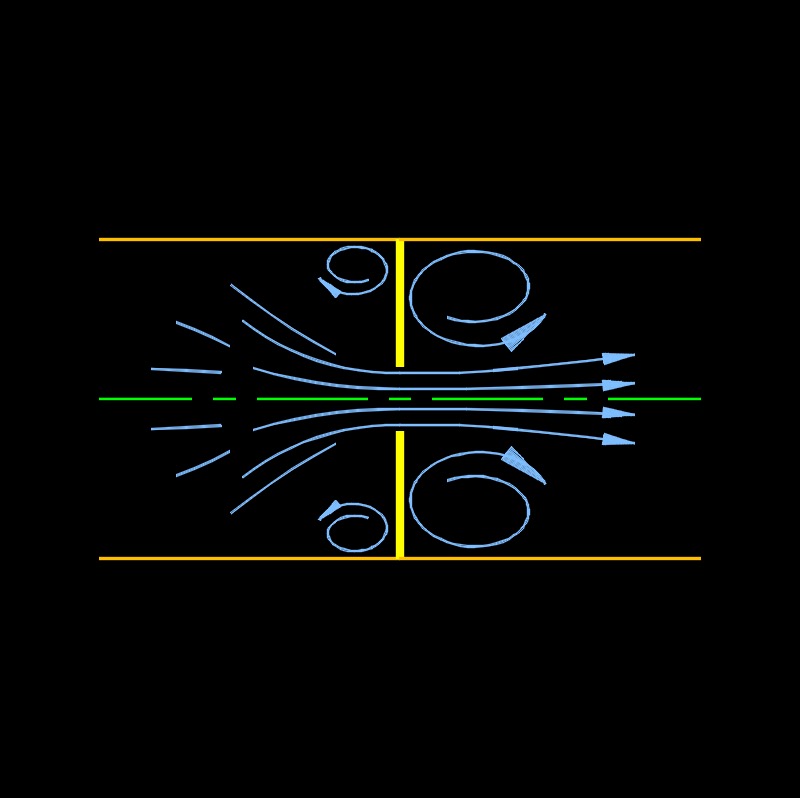
Water Flow Rate Through an Orifice

on 07 April 2016. Posted in Fluid Dynamics

orifice 1

Water Flow Rate Through an Orifice formula
\( Q_w \;=\; 0.0865 \; C_d \; ( d_o\;/\;4.654 )^2 \; \sqrt{ p_1 - p_2 \;/\; SG } \)
Symbol	English	Metric
\( Q_w \) = Water Flow Rate	\(ft^3\;/\;se\)	\(m^3\;/\;s\)
\( C_d \) = Orifice Discharge Coefficient	\(dimensionless\)	\(dimensionless\)
\( d_o \) = Orifice Diameter	\( in \)	\( mm \)
\( p_1 \) = Primary Pressure	\(lbf\;/\;in^2\)	\(Pa\)
\( p_2 \) = Secondary Pressure	\(lbf\;/\;in^2\)	\(Pa\)
\( SG \) = Water Specific Gravity	\(dimensionless\)	\(dimensionless\)

P D Logo 1