Borda-Carnot Equation

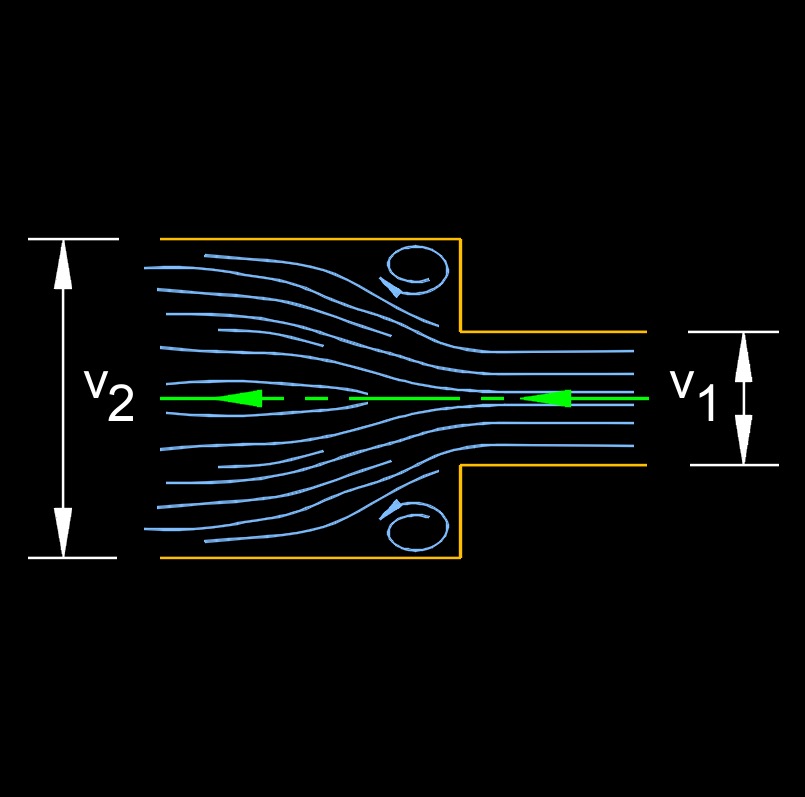Borda-Carnot equation is a empirical description of the mechanical loss energy losses of the fluid due to a sudden flow expansion.  It describes how the total head losses due to the expansion.  This equation is only valid for expansion, in the case of a contraction, the Borda-Carnot Equation cannot be used as it would indicate that energy is created.   The empirical loss coefficient, \(\large{\epsilon}\), is a number between 0 and 1.  For an abrupt and wide expansion, \(\large{\epsilon}\) is equal to 1.  For other instances, the value should be determined through empirical means.

 

Borda-Carnot equation
\( \Delta E = \frac { 1 }{ 2 } \; \epsilon \; \rho \; \left({v_1 - v_2}\right)^2 \)
Symbol	English	Metric
\( \Delta E \) = Fluid Mechanical Energy Loss	\( lbf-ft \)	\(J\)
\( \epsilon \)  (Greek symbol epsilon) = Empirical Loss Coefficient	\( dimensionless \)	\( dimensionless \)
\( \rho \)  (Greek symbol rho) = Fluid Density	\(lbm\;/\;ft^3\)	\(kg\;/\;m^3\)
\( v_1 \) = Mean Flow Velocity before Expansion	\(ft\;/\;sec\)	\(m\;/\;s\)
\( v_2 \) = Mean Flow Velocity after Expansion	\(ft\;/\;sec\)	\(m\;/\;s\)