Flow

Flow Types

Annular Flow  -  Annular flow is a two-phase flow regime where the liquid forms a film of varying thickness along the wall of the pipe and the vapor phase flows at a higher speed down the middle of the pipe.  The interface between the vapor and liquid phase is not entirely well defines.  Part of the liquid is sheared off from the film by the vapor and is carried along in the core as entrained droplets.  At the same time, turbulent eddies in the vapor deposit droplets on the liquid film.  Due to the different forces on the fluid, the thickness of the liquid film is not constant across the cross section of the pipe.  The effects of gravity can cause the thickness of the fluid film towards the bottom of the annulus to be bigger than the top.  Downstream of bends, most of the liquid will be at the outer wall.
Bubble Flow  -  Bubble flow occurs when liquid occupies the bulk of the cross-section and vapor flows in the form of bubbles along the top of the pipe.  During this phase the vapor and liquid velocities are about the same.
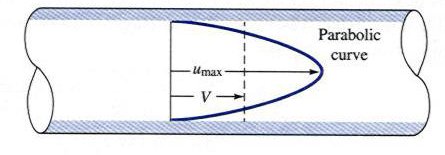
Laminar Flow  -  Laminar flow generally happens when dealing with low Reynolds Numbers in pipes.  This could be due to low velocities, large diameters or high viscosities.  Laminar flow can be modeled as a series of liquid cylinders in the pipe, where the innermost parts flow the fastest, and the cylinder touching the pipe isn't moving at all.

Shear stress in laminar flow is independent of the density - ρ, and the shear stress depends almost only on the viscosity - μ.

Plug Flow  -  The bubbles in the pipe eventually coalesce as the vapor rate increases.  Plug flow is similar to slug flow but liquid is the continuous phase along the bottom of the pipe.
Slug Flow  -  Slug flow occurs when the speed of the vapor phase pushes the waves from the wavy flow regime onto each other.  The waves grow until the liquid waves touch the top of the pipe and form frothy slugs.  The velocity of frothy slugs and the "slugs" of vapor is faster than the liquid velocity.  Slug flow is found in lower velocities in piping running uphill than in horizontal piping.  When running downhill, it takes higher vapor rates to establish slug flow than in horizontal pipe.  Because the slugs are moving faster than the average liquid velocity, care should be taken to avoid slug flow around fittings.  Severe water hammer may occur when changing flow direction when slug flow is occurring.
Spray Flow  -  Spray flow is also known as mist or dispersed flow occurs when two-phase flow where the liquid phase is the dispersed phase and exists in the form of many droplets, while the gas phase is the continuous phase.  This occurs when the velocity of the vapor tears the liquid film away from the wall and is carried by the vapor as entrained droplets.  Sprays are formed for industrial, commercial, agricultural, and power generation purposes by injection of a liquid stream into a gaseous environment.  In addition, sprays can form naturally in a falling or splashing liquid.
Stratified Flow  -  As the vapor rate continues to increase, the plugs join and become a continuous phase.  In fully stratified flow, vapor flows along the top of the pipe and liquid flows along the bottom.  The interface between the two phases is relatively smooth and the flow area occupied by each phase remains constant.  In uphill flow, stratified flow rarely occurs with wavy flow being favored.
Wavy Flow  -  As the vapor rate increases even more in the pipe during stratified flow, the top most layer begins to form waves.  As the vapor rate increases, the amplitude of the waves increases.  Wavy flow can occur when flow moves uphill, in horizontal pipe or in downhill flow.  Most often, it is found in piping that is horizontal but it may occur in uphill flow.  When the flow is moving downhill, wavy flow can still occur but the amplitude of the waves is not as great.

Flow Area

Flow area refers to the cross section area of the flow within the channel.