Bulk Modulus Formula |
||
|
\( K \;=\; p \cdot \dfrac{ V_i }{ V_c } \) (Bulk Modulus) \( p \;=\; \dfrac{ K \cdot V_c }{ V_i }\) \( V_i \;=\; \dfrac{ K \cdot V_c }{ p }\) \( V_c \;=\; \dfrac{ p \cdot V_i }{ K }\) |
||
| Symbol | Metric | Metric |
| \( K \) = Bulk Modulus | \(lbm \;/\; in^2\) | \( Pa \) |
| \( p \) = Pressure (psi) | \(lbf \;/\; in^2\) | \( Pa \) |
| \( V_i \) = Initial Volume | \( in^3 \) | \( mm^3 \) |
| \( V_c \) = Volume Change | \( in^3 \) | \( mm^3 \) |
Bulk modulus, abbreviated as B or K, also called bulk modulus of elasticity or modulus of volume expansion, is the elastic relationship between an applied pressure that acts to change the volume of the substance and the ability of a substance to withstand changes in volume when under compression.
- See Article - Bulk Modulus of an Element
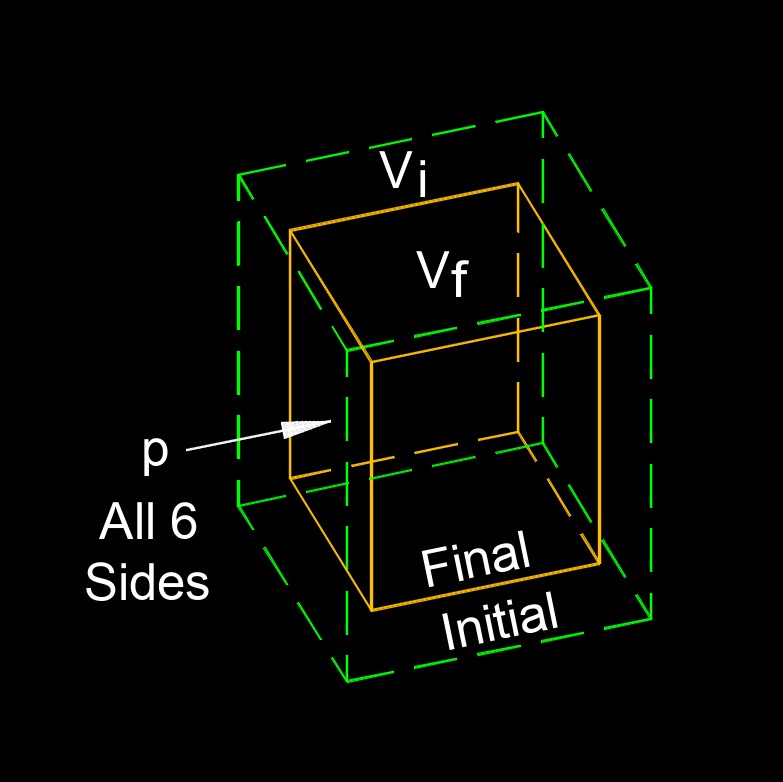
When a material is subjected to uniform external pressure, it tends to compress or contract in volume. The bulk modulus measures the ratio of the applied pressure to the resulting relative change in volume.
Most liquids like oil or water are considered incompressible. In practice, all materials are compressible to a certain extent. The bulk modulus of a liquid is the measure of compression with an increase in pressure. Materials with a high bulk modulus are relatively incompressible and resist volume changes under pressure, while materials with a low bulk modulus are more compressible and exhibit significant volume changes under pressure. For example, gases have low bulk modulus values, meaning they can be easily compressed, whereas solids such as metals have high bulk modulus values, indicating their resistance to compression.
