Head

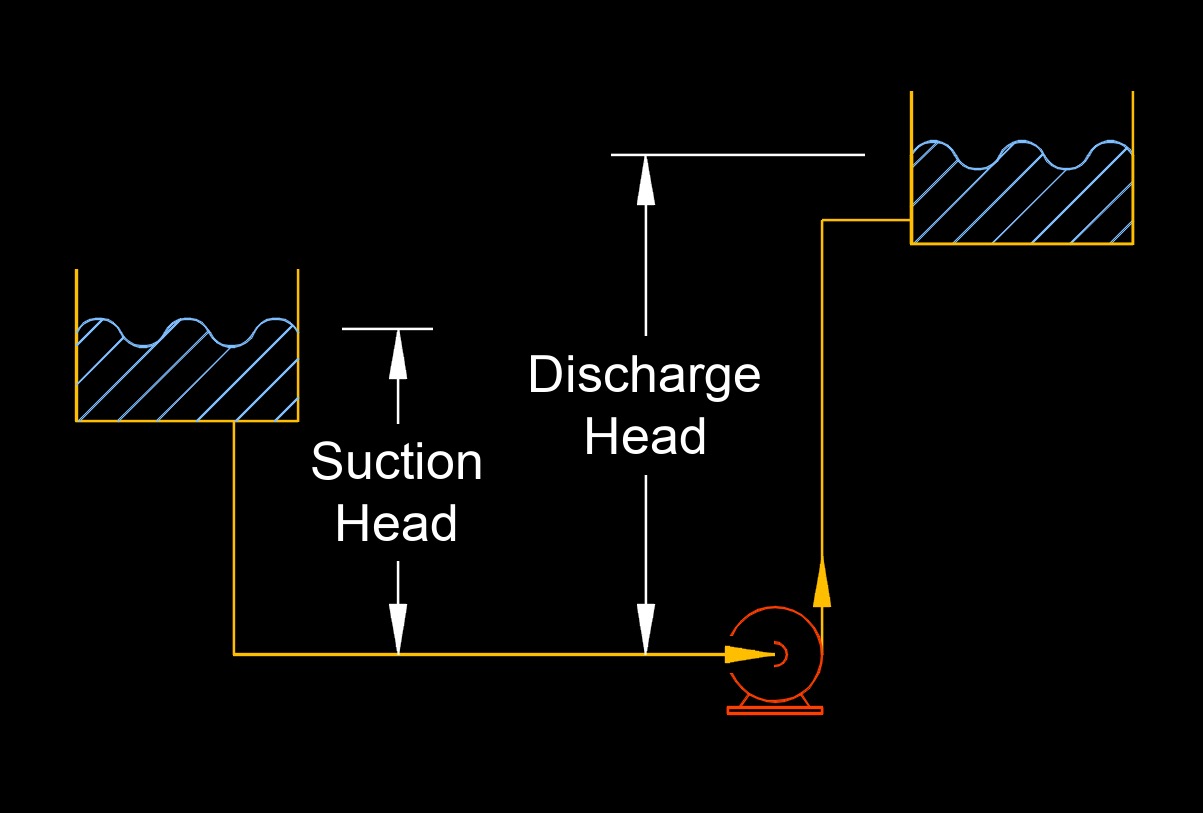Head, abbreviated as \(h\), is used to express pressure or pressure energy. 

Static head, abbreviated as \(h_s\), is the distance from the centerline of the gauge and above, to the surface of the liquid or you could say the difference in elevation.  The gauge in the pipe measures the pressure created by the weight of the liquid that is above the centerline of the gauge.

The gauge measures the static pressure of the static head.  The static preasure is less than the static head because of the loss of fluid friction and head velocity which the gauge can not measure.