Trapezoid
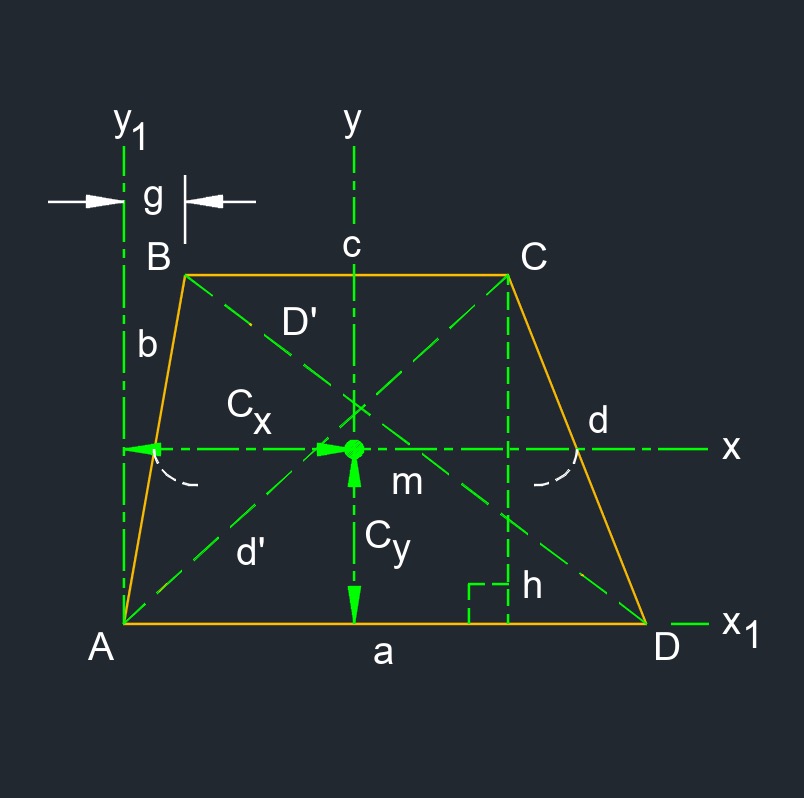 Trapezoid (a two-dimensional figure) is a quadrilateral that has a pair of parallel opposite sides.
Trapezoid (a two-dimensional figure) is a quadrilateral that has a pair of parallel opposite sides.- Acute angle measures less than 90°.
- Diagonal is a line from one vertices to another that is non adjacent.
- No interior angles are equal.
- Obtuse angle measures more than 90°.
- Quadrilateral (a two-dimensional figure) is a polygon with four sides.
- a & c are bases
- b & d are legs
- a ∥ c
- a ≠ c
- ∠A + ∠B = 180°
- ∠C + ∠D = 180°
- 2 diagonals
- 4 edges
- 4 vertexs
- See Article Links - Geometric Properties of Structural Shapes
- Tags: Structural Steel Quadrilateral
Trapezoid Index
- Area of a Trapezoid
- Diagonal of a Trapezoid
- Distance from Centroid of a Trapezoid
- Elastic Section Modulus of a Trapezoid
- Height of a Trapezoid
- Midline of a Trapezoid
- Perimeter of a Trapezoid
- Plastic Section Modulus of a Trapezoid
- Polar Moment of Inertia of a Trapezoid
- Radius of Gyration of a Trapezoid
- Second Moment of Area of a Trapezoid
- Edge of a Trapezoid
