Hydrostatic Pressure Formula |
||
|
\( HP \;=\; \rho \cdot g \cdot h + p_e \) (Hydrostatic Pressure) \( \rho \;=\; \dfrac{ HP - p_e }{ g \cdot h }\) \( g \;=\; \dfrac{ HP - p_e }{ \rho \cdot h }\) \( h \;=\; \dfrac{ HP - p_e }{ \rho \cdot g }\) \( p_e \;=\; HP - \rho \cdot g \cdot h \) |
||
| Symbol | English | Metric |
| \( HP \) = Hydrostatic Pressure (psi) | \(lbf \;/\; in^2\) | \(Pa\) |
| \( \rho \) (Greek symbol rho) = Fluid Density | \(lbm \;/\; ft^3\) | \(kg \;/\; m^3\) |
| \( g \) = Gravitational Acceleration | \(ft \;/\; sec^2\) | \(m \;/\; s^2\) |
| \( h \) = Fluid Height | \(ft\) | \(m\) |
| \( p_e \) = External Pressure (psi) | \(lbf \;/\; in^2\) | \(Pa\) |
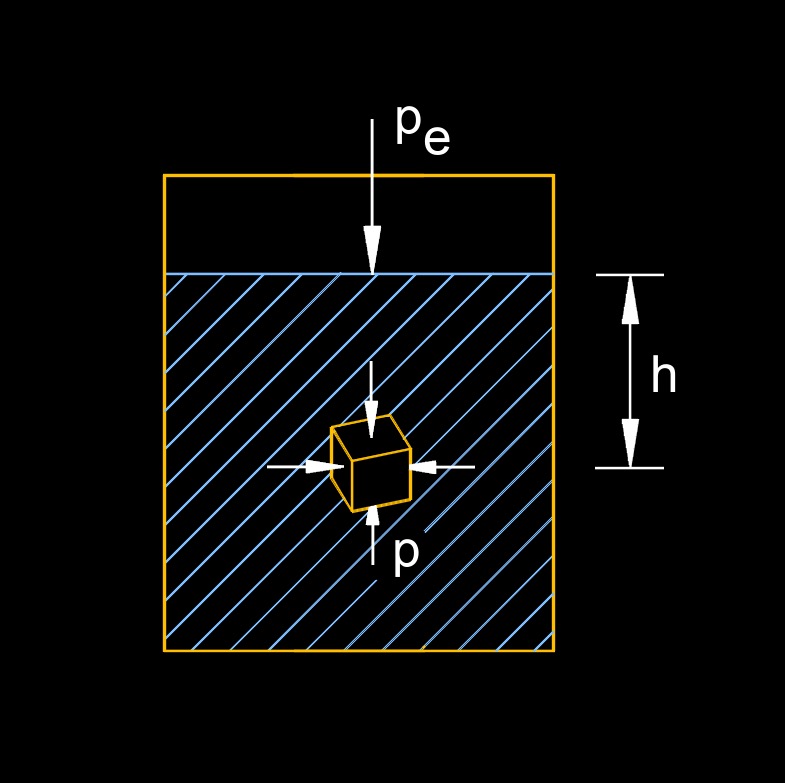 Hydrostatic pressure, abbreviated as HP, is the pressure a fluid exerts on an immersed object floating at a certain depth in a liquid. It is a concept in fluid mechanics and is related to the density of the fluid and the height of the fluid column.
Hydrostatic pressure, abbreviated as HP, is the pressure a fluid exerts on an immersed object floating at a certain depth in a liquid. It is a concept in fluid mechanics and is related to the density of the fluid and the height of the fluid column.
Key Points about Hydrostatic Pressure
- It increases with the depth of the fluid. The deeper you go in a fluid, the higher the hydrostatic pressure becomes.
- It depends on the density of the fluid. Denser fluids exert greater hydrostatic pressure for a given depth.
- It is directly proportional to the depth of the fluid. If you double the depth, you will double the hydrostatic pressure.
- Hydrostatic pressure is a scalar quantity, which means it has magnitude but no direction. It acts equally in all directions at a specific depth in a fluid.
This concept is important in various applications, including fluid dynamics, engineering, and geophysics, where it helps explain phenomena such as the pressure increase as you dive deeper underwater or the pressure changes in the Earth's crust due to the weight of overlying rocks and sediments.
