- See Article - Beam Design Formulas
Overhanging Beam - Point Load Between Supports at Any Point formulas |
||
|
\( R_1 \;=\; V_1 \; ( max.\; when\; a < b) \;=\; \dfrac{ P\cdot b }{ L } \) \( R_2 \;=\; V_2 \; (max. \;when\; a > b ) \;=\; \dfrac{ P\cdot a }{ L } \) \( M_{max} \; \left(at \;point \;of \;load \right) \;=\; \dfrac{ P\cdot a\cdot b }{ L } \) \( M_x \; \left( x < a \right) \;=\; \dfrac{ P\cdot b\cdot x }{ L } \) \( \Delta_{x_1} \;=\; \dfrac{ P\cdot a\cdot b\cdot x_1 }{ 6\cdot \lambda\cdot I\cdot L } \cdot ( L + a ) \) \( \Delta_a \; (at\; point \;of \;load ) \;=\; \dfrac{ P\cdot a^2\cdot b^2 }{ 3\cdot \lambda\cdot I\cdot L } \) \( \Delta_x \; (when\; x < a ) \;=\; \dfrac{ P\cdot b\cdot x }{ 6\cdot \lambda\cdot I\cdot L } \cdot ( L^2 - b^2 - x^2 ) \) \( \Delta_x \; ( when\; x > a ) \;=\; \dfrac{ P\cdot a \cdot ( L - x ) }{ 6\cdot \lambda\cdot I\cdot L } \cdot ( 2\cdot L\cdot x - x^2 - a^2 ) \) \( \Delta_{max} \; (at\; x = \sqrt{ \frac{ a \; (a + 2\;b ) }{3} } \; when\; a > b) \;=\; \dfrac{P\cdot a\cdot b \cdot ( a + 2\cdot b ) \cdot \sqrt{ 3\cdot a \cdot ( a + 2\cdot b) } }{ 27\cdot \lambda \cdot I\cdot L } \) |
||
| Symbol | English | Metric |
| \( \Delta \) = deflection or deformation | \(in\) | \(m\) |
| \( x \) = horizontal distance from reaction to point on beam | \(in\) | \(m\) |
| \( M \) = maximum bending moment | \(lbf-in\) | \(N-mm\) |
| \( V \) = maximum shear force | \(lbf\) | \(N\) |
| \( \lambda \) (Greek symbol lambda) = modulus of elasticity | \(lbf\;/\;in^2\) | \(Pa\) |
| \( R \) = reaction load at bearing point | \(lbf\) | \(N\) |
| \( I \) = second moment of area (moment of inertia) | \(in^4\) | \(m^4\) |
| \( L \) = span length of the bending member | \(in\) | \(m\) |
| \( P \) = total concentrated load | \(lbf\) | \(N\) |
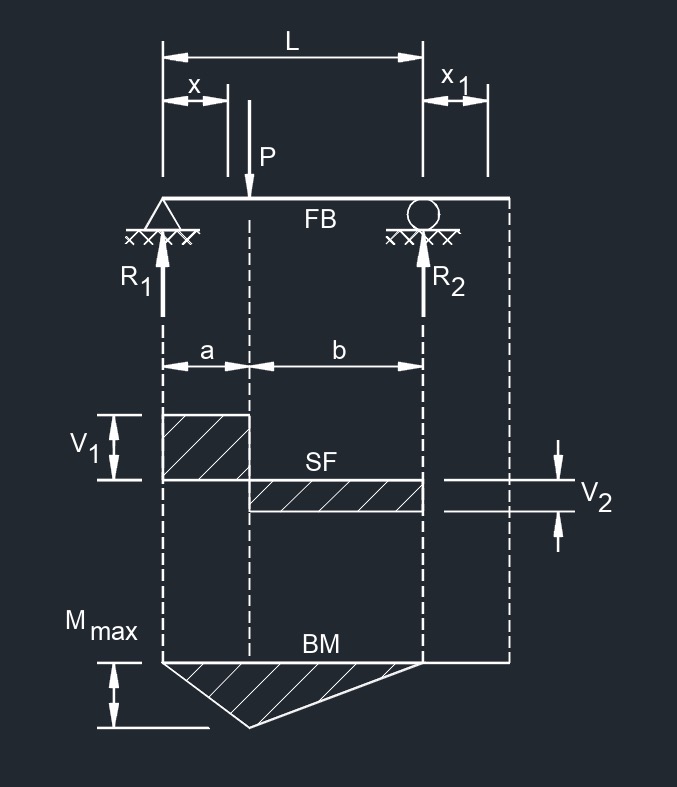
Diagram Symbols
Bending moment diagram (BMD) - Used to determine the bending moment at a given point of a structural element. The diagram can help determine the type, size, and material of a member in a structure so that a given set of loads can be supported without structural failure.
Free body diagram (FBD) - Used to visualize the applied forces, moments, and resulting reactions on a structure in a given condition.
Shear force diagram (SFD) - Used to determine the shear force at a given point of a structural element. The diagram can help determine the type, size, and material of a member in a structure so that a given set of loads can be supported without structural failure.
Uniformly distributed load (UDL) - A load that is distributed evenly across the entire length of the support area.
