- See Article - Geometric Properties of Structural Shapes
area of a Tapered Channel formula |
||
| \( A \;=\; t + a \cdot \left( s + n \right) \) | ||
| Symbol | English | Metric |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( n \) = thickness | \( in \) | \( mm \) |
| \( s \) = thickness | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( a \) = width | \( in \) | \( mm \) |
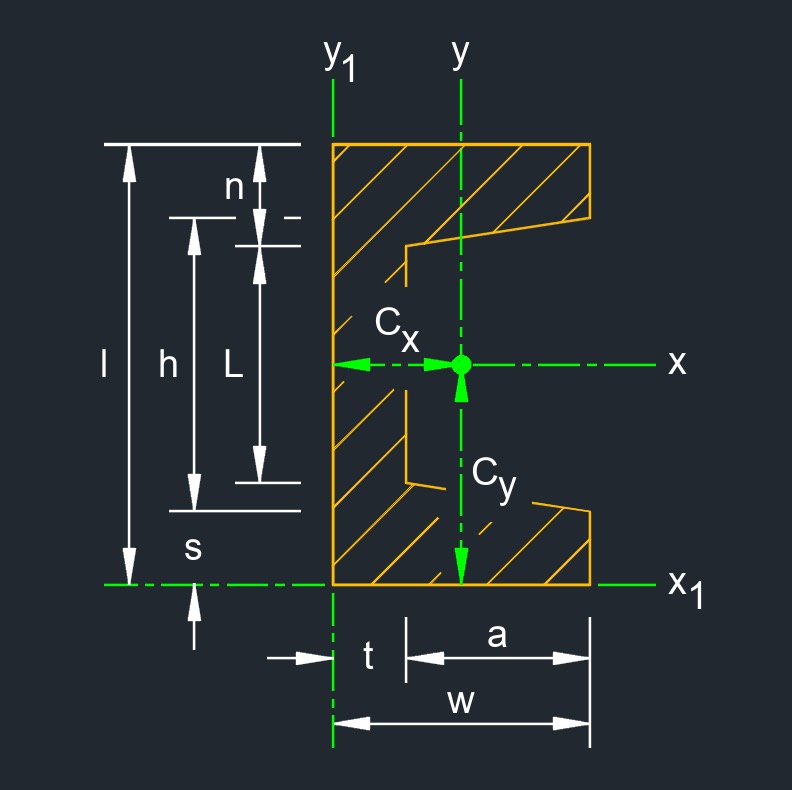Tapered channel, also called tapered C-channel or tapered U-channel, is a type of structural steel member with a cross-sectional shape resembling the letter "C" or "U" that gradually changes dimensions along its length. Unlike a standard C-channel or U-channel, where the sides are parallel and of constant dimensions, a tapered channel has sides that converge or diverge, resulting in a non-uniform cross-section. Tapered channels are used in situations where the structural requirements, load distribution, or other engineering considerations change along the length of the member. The tapering can be gradual or more pronounced, depending on the specific needs of the project.
Distance from Centroid of a Tapered Channel formulas |
||
|
\( C_x \;=\; \dfrac{1}{3} \cdot \left[ w^2 \cdot s + \dfrac{h\cdot t^2}{2} - \dfrac{\dfrac{h - L}{2\cdot \left(w - t \right) } }{3} \cdot \left( w + 2\cdot t \right) \cdot \left( w - t \right)^2 \right] \) \( C_y \;=\; \dfrac{l}{2} \) |
||
| Symbol | English | Metric |
| \( C \) = distance from centroid | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( L \) = height | \( in \) | \( mm \) |
| \( s \) = thickness | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
Elastic Section Modulus of a Tapered Channel formulas |
||
|
\( S_x \;=\; \dfrac{ I_x }{ C_y } \) \( S_y \;=\; \dfrac{ I_y }{ C_x } \) |
||
| Symbol | English | Metric |
| \( S \) = elastic section modulus | \( in^3 \) | \( mm^3 \) |
| \( C \) = distance from centroid | \( in \) | \( mm \) |
| \( I \) = moment of inertia | \( in^4 \) | \( mm^4 \) |
Perimeter of a Tapered Channel formula |
||
| \( P \;=\; 2\cdot a^2 + 2\cdot w + 2\cdot h - 2\cdot L^2 + L + 2\cdot s \) | ||
| Symbol | English | Metric |
| \( P \) = perimeter | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( L \) = height | \( in \) | \( mm \) |
| \( s \) = thickness | \( in \) | \( mm \) |
| \( a \) = width | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
Polar Moment of Inertia of a Tapered Channel formulas |
||
|
\( J_z \;=\; I_x + I_y \) \( J_{z1} \;=\; I_{x1} + I_{y1} \) |
||
| Symbol | English | Metric |
| \( J \) = torsional constant | \( in^4 \) | \( mm^4 \) |
| \( I \) = moment of inertia | \( in^4 \) | \( mm^4 \) |
Radius of Gyration of a Tapered Channel formulas |
||
|
\( k_x \;=\; \sqrt{ \dfrac{ \dfrac{1}{12} \cdot \left[ w\cdot l^3 + \dfrac{1}{8\cdot \dfrac{h - L}{2\cdot \left(w - t \right)}} \cdot \left( h^4 - L^4 \right) \right] }{ l \cdot t + a \cdot \left( s + n \right) } } \) \( k_y \;= \; \sqrt{ \dfrac{ \dfrac{1}{3} \cdot \left[ 2\cdot s\cdot w^3\cdot L\cdot t^3 + \dfrac{\dfrac{h - L}{2\cdot \left(w - t \right)}}{2} \cdot \left( w^4 - t^4 \right) \right] - A \cdot \left( w - y \right)^2 }{ l\cdot t + a\cdot \left( s + n \right) } } \) \( k_z \;=\; \sqrt{ k_{x}{^2} + k_{y}{^2} } \) \( k_{x1} \;=\; \sqrt{ \dfrac{ I_{x1} }{A} } \) \( k_{y1} \;=\; \sqrt{ \dfrac{ I_{y1} }{A} } \) \( k_{z1} \;=\; \sqrt{ k_{x1}{^2} + k_{y1}{^2} } \) |
||
| Symbol | English | Metric |
| \( k \) = radius of gyration | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( L \) = height | \( in \) | \( mm \) |
| \( s \) = thickness | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( a \) = width | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
Second Moment of Area of a Tapered Channel formulas |
||
|
\( I_x \;=\; \dfrac{1}{12} \cdot \left[ w\cdot l^3 + \dfrac{1}{8\cdot \dfrac{h - L}{2\cdot \left(w - t \right) }} \cdot \left( h^4 - L^4 \right) \right] \) \( I_y \;=\; \dfrac{1}{3} \cdot \left[ 2\cdot s\cdot w^3 + L\cdot t^3 + \dfrac{\dfrac{h - L}{2\cdot \left(w - t \right) }}{2} \cdot \left( w^4 - t^4 \right) \right] - A \cdot \left( w - y \right)^2 \) \( I_{x1} \;=\; l_x + A\;C_y \) \( I_{y1} \;=\; l_y + A\;C_x \) |
||
| Symbol | English | Metric |
| \( I \) = moment of inertia | \( in^4 \) | \( mm^4 \) |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( C \) = distance from centroid | \( in \) | \( mm \) |
| \( h \) = height | \( in \) | \( mm \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( L \) = height | \( in \) | \( mm \) |
| \( s \) = thickness | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |
Torsional Constant of a Tapered Channel formula |
||
| \( J \;=\; \dfrac{ 2 \cdot \left( w - \dfrac {t}{2} \right) \cdot n^3 \cdot \left( l - n \right) \cdot t^3 }{3} \) | ||
| Symbol | English | Metric |
| \( J \) = torsional constant | \( in^4 \) | \( mm^4 \) |
| \( l \) = height | \( in \) | \( mm \) |
| \( n \) = thickness | \( in \) | \( mm \) |
| \( s \) = thickness | \( in \) | \( mm \) |
| \( t \) = thickness | \( in \) | \( mm \) |
| \( w \) = width | \( in \) | \( mm \) |