HomeEngineeringCivilStructuralTapered T Beam
Print

Tapered T Beam

on . Posted in Structural Engineering

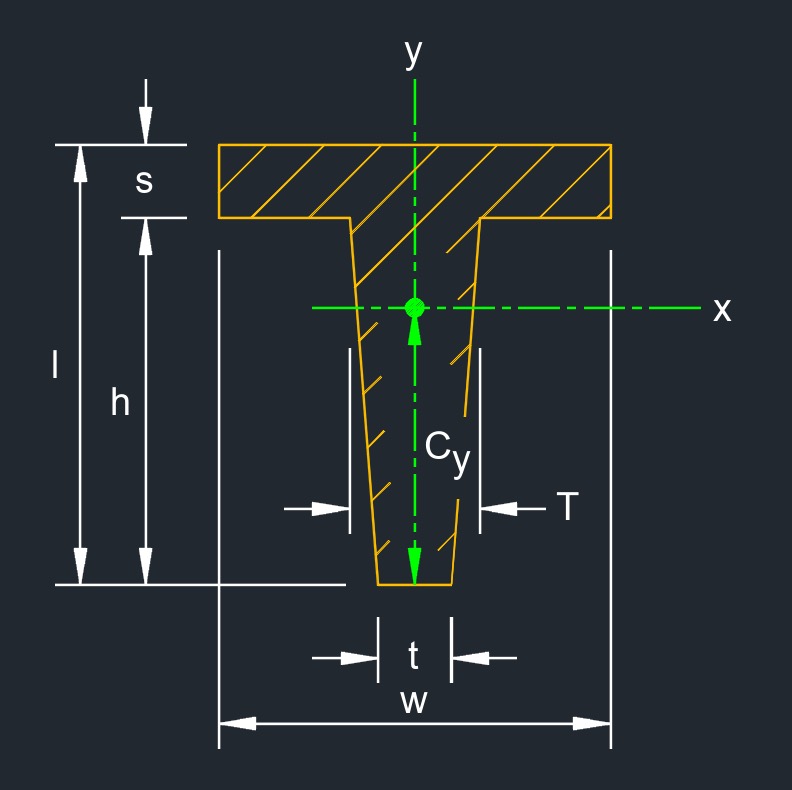T beam tapered 1Tapered T-beam, also c tapered teealled beam, is a type of structural beam with a T-shaped cross-sectional profile that changes dimensions along its length.  This means that the stem of the T-beam gradually becomes narrower or wider as the beam extends from one end to the other.  The tapering of the beam's dimensions can be subtle or more pronounced, depending on the specific engineering requirements of the structure.

Tapered T-beams are often used in situations where the load distribution, spans, or other design considerations change along the length of the beam. This design allows for optimization of materials and structural performance while accommodating varying loads.

Tapered T Beam Index

 

area of a Tapered T Beam formula
\(\large{ A =  w\;s  +  \frac{ h \; \left(T  \;+\;  t \right) }{2}   }\) 
Symbol English Metric
\(\large{ A }\) = area \(\large{ in^2 }\) \(\large{ mm^2 }\)
\(\large{ h }\) = height  \(\large{ in }\)  \(\large{ mm }\)
\(\large{ t }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ T }\) = thickness  \(\large{ in }\) \(\large{ mm }\)
\(\large{ s }\) = width  \(\large{ in }\) \(\large{ mm }\)
\(\large{ w }\) = width \(\large{ in }\) \(\large{ mm }\)

 

Distance from Centroid of a Tapered T Beam formulas

 \(\large{ C_x =  0  }\)

\(\large{ C_y =  l \;-\; \frac{1}{6\;A} \;  \left[    3\;w\;s^2  +  3\;h\;t  \; \left( l  +  s \right)  +  h \; \left( T - t \right) \; \left( h  +  3\;s \right)   \right]   }\) 
Symbol English Metric
\(\large{ C }\) = distance from centroid  \(\large{ in }\)  \(\large{ mm }\)
\(\large{ A }\) = area \(\large{ in^2 }\) \(\large{ mm^2 }\)
\(\large{ h }\) = height  \(\large{ in }\)  \(\large{ mm }\)
\(\large{ l }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ t }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ T }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ s }\) = width  \(\large{ in }\) \(\large{ mm }\)
\(\large{ w }\) = width \(\large{ in }\) \(\large{ mm }\)

 

Elastic section Modulus of a Tapered T Beam formual
\(\large{ S_{x} =  \frac{ I_{x} }{ C_{y}   } }\) 
Symbol English Metric
\(\large{ S }\) = elastic section modulus \(\large{ in^3 }\) \(\large{ mm^3 }\)
\(\large{ C }\) = distance from centroid \(\large{ in }\) \(\large{ mm }\)
\(\large{ I }\) = moment of inertia \(\large{ in^4 }\) \(\large{ mm^4 }\)

 

Perimeter of a Tapered T Beam formula
\(\large{ P =  2\;w  +  2\;s \;-\; T  +  t  +  2\;  \sqrt{   \left( \frac{1}{2} \right)^2  +  \left( \frac{T}{2} \right)^2       }   }\) 
Symbol English Metric
\(\large{ P }\) = perimeter  \(\large{ in }\)  \(\large{ mm }\)
\(\large{ t }\) = thickness  \(\large{ in }\)  \(\large{ mm }\)
\(\large{ T }\) = thickness  \(\large{ in }\)  \(\large{ mm }\)
\(\large{ s }\) = width  \(\large{ in }\) \(\large{ mm }\)
\(\large{ w }\) = width \(\large{ in }\) \(\large{ mm }\)

 

Radius of Gyration of a Tapered T Beam formulas

\(\large{ k_{x} =  \sqrt{  \frac{ I_x }{ A  }   }   }\) 

\(\large{ k_{x1} =  \sqrt{  \frac{ I_{x1} }{ A  }   }   }\) 
Symbol English Metric
\(\large{ k }\) = radius of gyration \(\large{ in }\) \(\large{ mm }\)
\(\large{ A }\) = area \(\large{ in^2 }\) \(\large{ mm^2 }\)
\(\large{ I }\) = moment of inertia \(\large{ in^4 }\) \(\large{ mm^4 }\)

 

Second Moment of Area of a Tapered T Beam formulas

\(\large{ I_{x} =   \frac{  \left[  4\;w\;s^3  \;+\;  h^3 \;  \left( 3\;t \;+\; T \right)  \right]    \;-\; A \; \left( l \;-\; C_y \;-\; s \right)^2   }{12}   }\) 

\(\large{ I_{x1} =  I_{x}  +  A \;C_{y} }\) 
Symbol English Metric
\(\large{ I }\) = moment of inertia \(\large{ in^4 }\) \(\large{ mm^4 }\)
\(\large{ A }\) = area \(\large{ in^2 }\) \(\large{ mm^2 }\)
\(\large{ C }\) = distance from centroid \(\large{ in }\) \(\large{ mm }\)
\(\large{ h }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ l }\) = height \(\large{ in }\) \(\large{ mm }\)
\(\large{ t }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ T }\) = thickness \(\large{ in }\) \(\large{ mm }\)
\(\large{ s }\) = width \(\large{ in }\) \(\large{ mm }\)
\(\large{ w }\) = width \(\large{ in }\) \(\large{ mm }\)

 

Piping Designer Logo 1

Tags: Structural Steel

Latest Articles