Isosceles Trapezoid
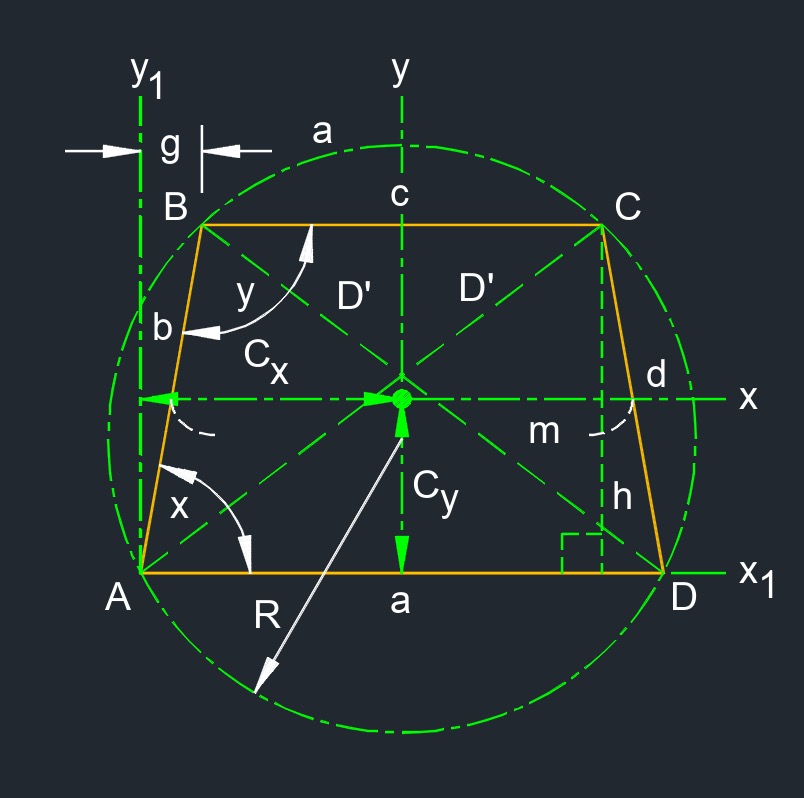Isosceles trapezoid (a two-dimensional figure) is a trapezoid with only one pair of parallel edges and having base angles that are the same.- Acute angle measures less than 90°.
- Circumcircle is a circle that passes through all the vertices of a two-dimensional figure.
- Diagonal is a line from one vertices to another that is non adjacent.
- Obtuse angle measures more than 90°.
- a & c are bases
- b & d are legs
- a ∥ c
- a ≠ c
- b = d
- ∠A & ∠D < 90°
- ∠B & ∠C > 90°
- ∠A = ∠D
- ∠B = ∠C
- ∠A + ∠B = 180°
- ∠C + ∠D = 180°
- ∠A + ∠C = 180°
- ∠B + ∠D = 180°
- 2 diagonals
- 4 edges
- 4 vertexs
- See Article Links - Geometric Properties of Structural Shapes
- Tags: Structural Steel Quadrilateral
Isosceles Trapezoid Index
- Angle of a Isosceles Trapezoid
- Area of an Isosceles Trapezoid
- Circumcircle of an Isosceles Trapezoid
- Diagonal of an Isosceles Trapezoid
- Distance from Centroid of an Isosceles Trapezoid
- Elastic Section Modulus of an Isosceles Trapezoid
- Height of an Isosceles Trapezoid
- Perimeter of an Isosceles Trapezoid
- Plastic Section Modulus of an Isosceles Trapezoid
- Polar Moment of Inertia of an Isosceles Trapezoid
- Radius of Gyration of an Isosceles Trapezoid
- Second Moment of Area of an Isosceles Trapezoid
Angle of a Isosceles Trapezoid formulas |
||
|
\(\large{ x = arccos \; \frac{\left(\frac{a \;-\; c}{2}\right)^2 \;+\; b^2 \;-\; h^2}{2\;\left(\frac{a \;-\; c}{2}\right)\;b} }\) \(\large{ y = 180° - x }\) |
||
| Symbol | English | Metric |
| \(\large{ x }\) = acute angle | \(\large{ deg }\) | \(\large{ deg }\) |
| \(\large{ y }\) = obtuse angle | \(\large{ deg }\) | \(\large{ deg }\) |
| \(\large{ a, b, c, d }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ h }\) = height | \(\large{ in }\) | \(\large{ mm }\) |
Area of an Isosceles Trapezoid formulas |
||
|
\(\large{ A_{area} = \frac {h}{2} \; \left(c + a \right) }\) \(\large{ A_{area} = h \left( \frac {c \;+\; a} {2 } \right) }\) \(\large{ A_{area} = mc \; sin \; x }\) \(\large{ A_{area} = mc \; sin \; y }\) |
||
| Symbol | English | Metric |
| \(\large{ A_{area} }\) = area | \(\large{ in^2 }\) | \(\large{ mm^2 }\) |
| \(\large{ m }\) = central median | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a, b, c, d }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ h }\) = height | \(\large{ in }\) | \(\large{ mm }\) |
Circumcircle of an Isosceles Trapezoid formulas |
||
|
\(\large{ R = \frac{ b\;D'\;c }{ 4 \;\sqrt { s \; \left( s \;-\; b \right) \; \left( s \;-\; D' \right) \left( s \;-\; c \right) } } }\) \(\large{ s = \frac {b \;+\; D' \;+\; c} {2} }\) \(\large{ R = \frac { b\; D' \;a } { 4 \;\sqrt { s \; \left( s \;-\; b \right) \; \left( s \;-\; D' \right) \left( s \;-\; a \right) } } }\) \(\large{ s = \frac {b \;+\; D' \;+\; a} {2} }\) \(\large{ R = b \; \sqrt{ \frac{a\;c \;+\; b^2}{4\;b^2 \;-\; \left( a \;-\; c \right)^2} } }\) |
||
| Symbol | English | Metric |
| \(\large{ R }\) = outside radius | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ D' }\) = diagonal | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a, b, c, d }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
Diagonal of an Isosceles Trapezoid formula |
||
| \(\large{ D' = \sqrt { b^2 \;+\; c\;a } }\) | ||
| Symbol | English | Metric |
| \(\large{ D' }\) = diagonal | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a, b, c, d }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ h }\) = height | \(\large{ in }\) | \(\large{ mm }\) |
Distance from Centroid of an Isosceles Trapezoid formulas |
||
|
\(\large{ C_x = \frac{ a }{ 2 } }\) \(\large{ C_y = \frac{ h }{ 3} \; \left( \frac { 2\;c \;+\; a } { c \;+\; a } \right) }\) |
||
| Symbol | English | Metric |
| \(\large{ C }\) = distance from centroid | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a, b, c, d }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ h }\) = height | \(\large{ in }\) | \(\large{ mm }\) |
Elastic Section Modulus of an Isosceles Trapezoid formulas |
||
|
\(\large{ S_x = \frac { I_x } { C_y } }\) \(\large{ S_y = \frac { I_y } { C_x } }\) |
||
| Symbol | English | Metric |
| \(\large{ S }\) = elastic section modulus | \(\large{in^3}\) | \(\large{ mm^3 }\) |
| \(\large{ C }\) = distance from centroid | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ I }\) = moment of inertia | \(\large{\frac{lbm}{ft^2-sec} }\) | \(\large{\frac{kg}{m^2} }\) |
Height of an Isosceles Trapezoid formula |
||
| \(\large{ h = \frac{1}{2} \; \sqrt { 4\;b^3 \;-\; {c \;+\; a} } }\) | ||
| Symbol | English | Metric |
| \(\large{ a, b, c, d }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ h }\) = height | \(\large{ in }\) | \(\large{ mm }\) |
Perimeter of an Isosceles Trapezoid formulas |
||
|
\(\large{ P = 2\;b + c + a }\) \(\large{ P = 2 \; \sqrt{ h^2 + \frac{\left(b \;-\; a\right)^2}{4} } + a + b }\) |
||
| Symbol | English | Metric |
| \(\large{ P }\) = perimeter | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a, b, c, d }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ h }\) = height | \(\large{ in }\) | \(\large{ mm }\) |
Plastic Section Modulus of an Isosceles Trapezoid formulas |
||
|
\(\large{ Z_x = \frac{ h \; \left( 2\;c^2 \;-\; c\;a \;+\; 2\;a^2 \right) }{ 12 } }\) \(\large{ Z_y = \frac{ h^2 \; \left( 11\;c^2 \;+\; 26\;c\;a \;+\; 11\;a^2 \right) }{ 48 \; \left( c \;+\; a \right) } }\) |
||
| Symbol | English | Metric |
| \(\large{ Z }\) = plastic section modulus | \(\large{ in^3 }\) | \(\large{ mm^3 }\) |
| \(\large{ a, b, c, d }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ h }\) = height | \(\large{ in }\) | \(\large{ mm }\) |
Polar Moment of Inertia of an Isosceles Trapezoid formulas |
||
|
\(\large{ J_{z} = I_x + I_y }\) \(\large{ J_{z1} = I_{x1} + I_{y1} }\) |
||
| Symbol | English | Metric |
| \(\large{ J }\) = torsional constant | \(\large{ in^4 }\) | \(\large{ mm^4 }\) |
| \(\large{ I }\) = moment of inertia | \(\large{ in^4 }\) | \(\large{ mm^4 }\) |
Radius of Gyration of an Isosceles Trapezoid formulas |
||
|
\(\large{ k_{x} = \frac{ h }{ 6 } \; \sqrt{ 2 + \frac{ 4\;c\;a}{ \left( c \;+\; a \right)^2 } } }\) \(\large{ k_{y} = \frac{ 1 }{ 12 } \; \sqrt{ 6 \left( c^2 + a^2 \right) } }\) \(\large{ k_{z} = \sqrt{ k_{x}{^2} + k_{y}{^2} } }\) \(\large{ k_{y1} = \sqrt{ \frac{ 3\;a \;+\; 5\;c}{ 12\; \left( a \;+\; c \right) } \;a } }\) \(\large{ k_{z1} = \sqrt{ k_{x1}{^2} + k_{y1}{^2} } }\) |
||
| Symbol | English | Metric |
| \(\large{ k }\) = radius of gyration | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a, b, c, d }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ h }\) = height | \(\large{ in }\) | \(\large{ mm }\) |
Second Moment of Area of an Isosceles Trapezoid formulas |
||
|
\(\large{ I_{x} = \frac{ h^3 \; \left( c^2 \;+\; 4\;c\;a \;+\; a^2 \right) }{ 36 \; \left( c \;+\; a \right) } }\) \(\large{ I_{y} = \frac{ h \; \left( c \;+\; a \right) \left( c^2 \;+\; a^2 \right) }{ 48 } }\) \(\large{ I_{x1} = \frac{ h^3 \; \left( 3\;c \;+\; a \right) }{ 12 } }\) \(\large{ I_{y1} = \frac{ h \; \left( c \;+\; a \right) \left( c^2 \;+\; 7\;a^2 \right) }{ 48 } }\) |
||
| Symbol | English | Metric |
| \(\large{ k }\) = radius of gyration | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ a, b, c, d }\) = edge | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ h }\) = height | \(\large{ in }\) | \(\large{ mm }\) |
| \(\large{ I }\) = moment of inertia | \(\large{ in^4 }\) | \(\large{ mm^4 }\) |
