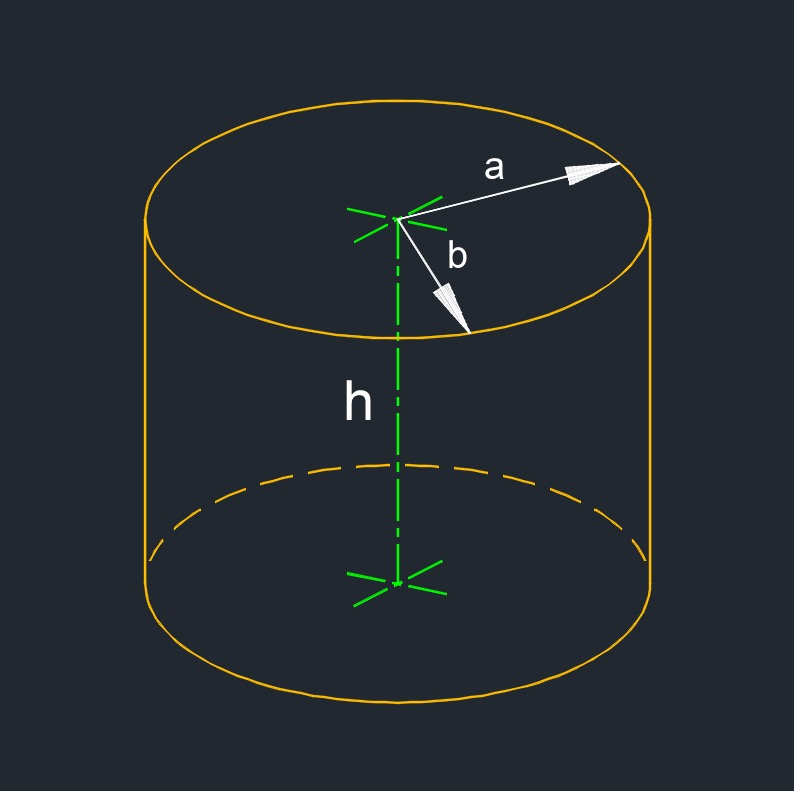Elliptic cylinder (a three-dimensional figure) has a cylinder shape with elliptical ends.- 2 bases
Since there is no easy way to calculate the ellipse perimeter with high accuracy. Calculating the laterial surface will be approximate also.
Lateral Surface Area of a Right Elliptic Cylinder formula
|
| \(\large{ A_l \approx h \; \left( 2\;\pi \;\sqrt {\; \frac{1}{2}\; \left(a^2 + b^2 \right) } \right) }\) |
| Symbol |
English |
Metric |
| \(\large{ A_l }\) = approximate lateral surface area (side) |
\(\large{ in^2 }\) |
\(\large{ mm^2 }\) |
| \(\large{ a }\) = length semi-major axis |
\(\large{ in }\) |
\(\large{ mm }\) |
| \(\large{ b }\) = length semi-minor axis |
\(\large{ in }\) |
\(\large{ mm }\) |
| \(\large{ h }\) = height |
\(\large{ in }\) |
\(\large{ mm }\) |
Surface Area of a Right Elliptic Cylinder formula
|
| \(\large{ A_s \approx h \; \left( 2\;\pi \;\sqrt {\; \frac{1}{2}\; \left(a^2 + b^2 \right) } \right) + 2\; \left( \pi \; a \; b \right) }\) |
| Symbol |
English |
Metric |
| \(\large{ A_s }\) = approximate surface area (bottom, top, side) |
\(\large{ in^2 }\) |
\(\large{ mm^2 }\) |
| \(\large{ a }\) = length semi-major axis |
\(\large{ in }\) |
\(\large{ mm }\) |
| \(\large{ b }\) = length semi-minor axis |
\(\large{ in }\) |
\(\large{ mm }\) |
| \(\large{ h }\) = height |
\(\large{ in }\) |
\(\large{ mm }\) |
Volume of a Right Elliptic Cylinder formula
|
| \(\large{ V = \pi\; a \;b\; h }\) |
| Symbol |
English |
Metric |
| \(\large{ V }\) = volume |
\(\large{ in^3 }\) |
\(\large{ mm^3 }\) |
| \(\large{ a }\) = length semi-major axis |
\(\large{ in }\) |
\(\large{ mm }\) |
| \(\large{ b }\) = length semi-minor axis |
\(\large{ in }\) |
\(\large{ mm }\) |
| \(\large{ h }\) = height |
\(\large{ in }\) |
\(\large{ mm }\) |
