Work Formula |
||
|
\( W \;=\; F \cdot d \) (Work) \( F \;=\; \dfrac{ W }{ d } \) \( d \;=\; \dfrac{ W }{ F } \) |
||
| Symbol | English | Metric |
| \( W \) = Work | \(lbf-ft\) | \(J\) |
| \( F \) = Force | \( lbf \) | \(N\) |
| \( d \) = Displacement | \( ft \) | \( m \) |
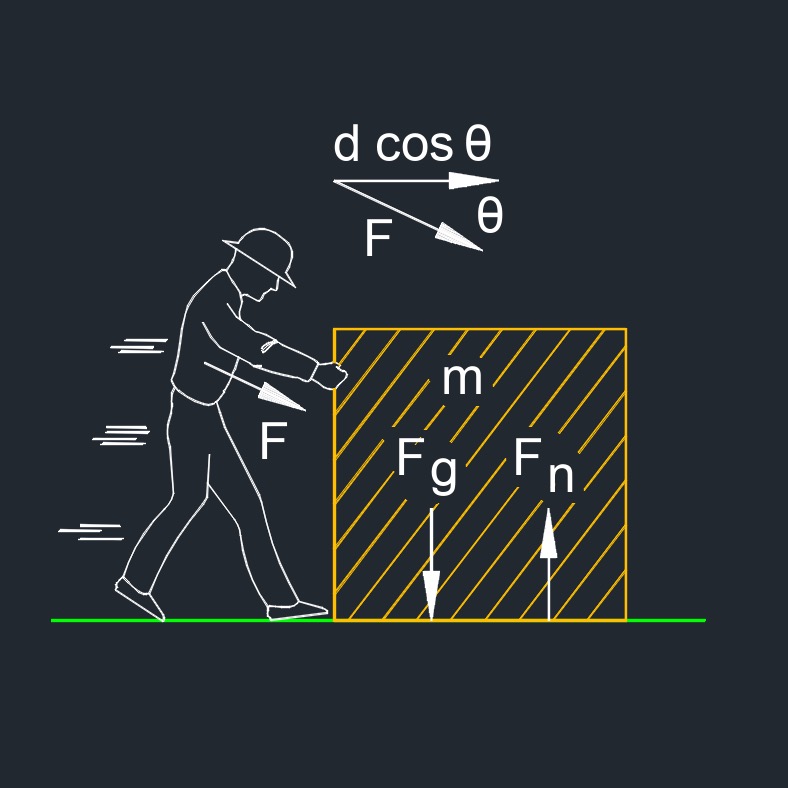Work, abbreviated as W, is action done or applied force on an object that displaces the object. If the applied force is straight down there is no work done. But if the applied force is at an angle the displacement will take more force. Work is a scalar quantity having magnitude and is independent of any specific direction.
Work Formula |
||
|
\( W \;=\; F \cdot d \cdot cos (\theta) \) (Work) \( F \;=\; \dfrac{ W }{ d \cdot cos (\theta) } \) \( d \;=\; \dfrac{ W }{ F \cdot cos (\theta) }\) \( cos (\theta) \;=\; \dfrac{ W }{ F \cdot d } \) |
||
| Symbol | English | Metric |
| \( W \) = Work | \(lbf-ft\) | \(J\) |
| \( F \) = Force | \( lbf \) | \(N\) |
| \( d \) = Displacement | \( ft \) | \( m \) |
| \( \theta \) = Angle | \(deg\) | \( rad \) |
Work is a scalar and can be positive or negative, Work is positive if the applied force is in the same direction as the displacement. Work is negative if the applied force is in the same direction opposite the displacement. The sign (+ or -) is important because it will tell if the speed of an object will increase or decrease as a result of appling the work.
