Velocity gradient formula |
||
|
\( \nu \;=\; \dfrac{ dv }{ dx }\) (Velocity Gradient) \( dv \;=\; \nu \cdot dx \) \( dx \;=\; \dfrac{ dv }{ \nu } \) |
||
| Symbol | English | Metric |
| \( \nu \) (Greek symbol nu) = Velocity Gradient | \(ft \;/\; sec\) | \(m \;/\; s\) |
| \( dv\) = Imperceptible Change in Velocity | \(ft \;/\; sec\) | \(m \;/\; s\) |
| \( dx \) = Imperceptible Distance Perpendicular Between Two Layers of Fluid | \(in\) | \(mm\) |
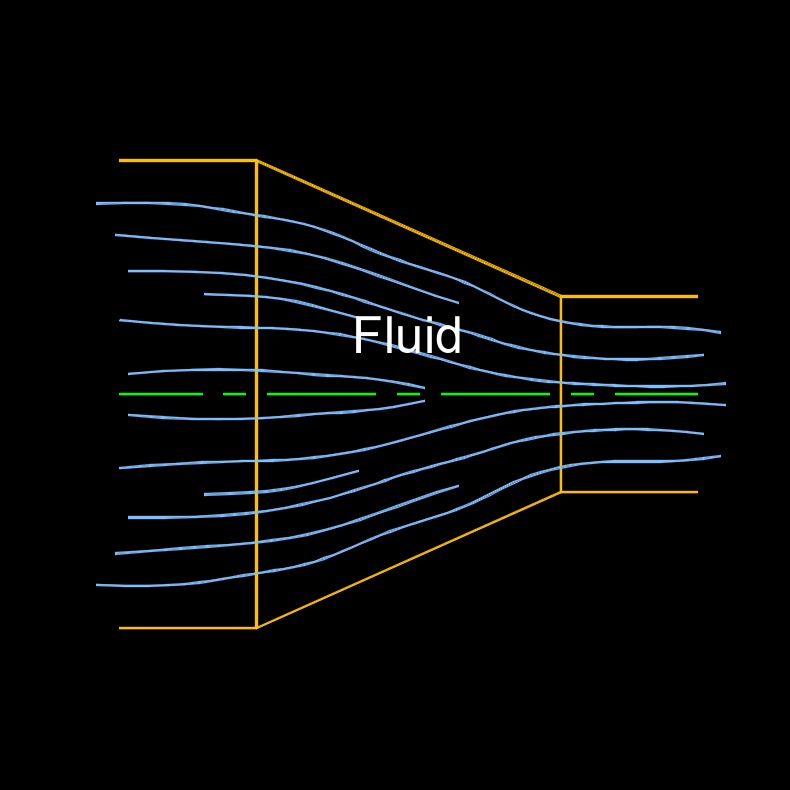
Velocity gradient, abbreviated as \(\nu\) (Greek symbol nu), is a measure of how the velocity of a fluid changes with respect to distance within the fluid. In other words, it quantifies the rate at which the fluid velocity changes from one point to another in the flow field. This is used in fluid dynamics and is particularly relevant in the study of viscous flows and shear stress.
