Reynolds Number

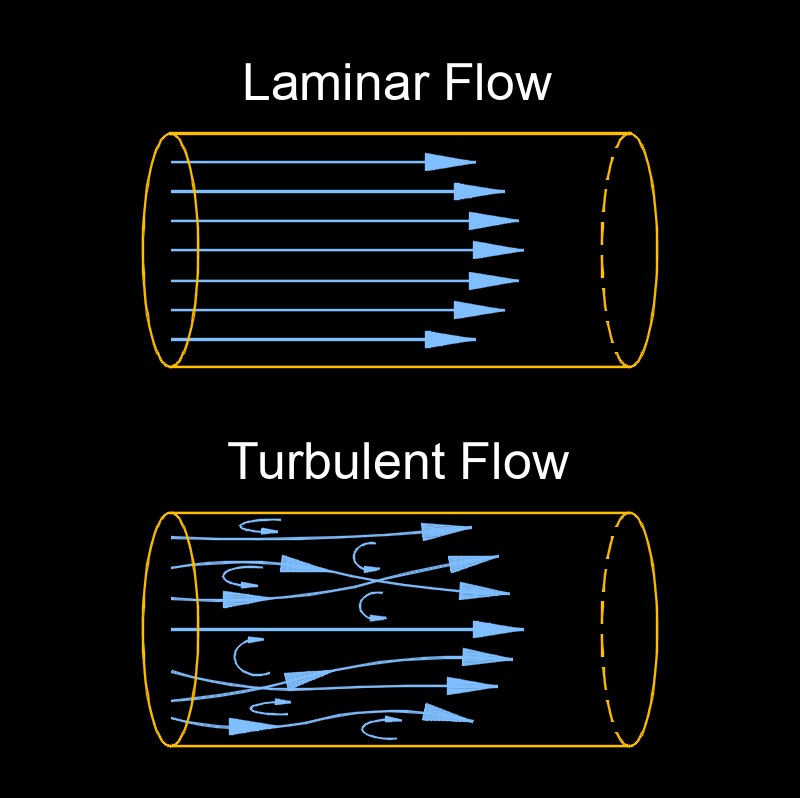
Reynolds number, abbreviated as Re, a dimensionless number, measures the ratio of inertial forces (forces that remain at rest or in uniform motion) to viscosity forces in the fluid flow (the resistance to flow).  It is used to predict the flow regimes of a fluid or gas.

The Reynolds number is commonly used in fluid dynamics to predict the onset of turbulence in a fluid flow.  At low Reynolds numbers (less than about 2300 for a pipe flow), the flow is laminar and exhibits smooth, ordered flow.  At high Reynolds numbers (greater than about 4000 for a pipe flow), the flow becomes turbulent and exhibits chaotic, irregular flow patterns.  The transition between laminar and turbulent flow depends on the specific system and the properties of the fluid.

Reynolds Number Categorizes Fluids into Different Regimes

Laminar Flow (Low Reynolds Numbers)

• Description  -  Laminar flow is characterized by smooth, orderly fluid motion with well defined layers that move parallel to each other.
• Reynolds Number Range  -  Typically, Reynolds numbers less than about 2,300 indicate laminar flow for pipe flow.  For other geometries, the transition may occur at different values.

Transitional Flow

• Description  -  Transitional flow occurs during the transition between laminar and turbulent flow.  It is characterized by the coexistence of laminar and turbulent patches.
• Reynolds Number Range  -  The transition from laminar to turbulent flow is gradual and not precisely defined.  It often occurs in the range of Reynolds numbers around 2,300 to 4,000 for pipe flow.

Turbulent Flow (High Reynolds Numbers)

• Description  -  Turbulent flow is characterized by chaotic, irregular fluid motion, with mixing, eddies, and vortices.
• Reynolds Number Range  -  Generally, Reynolds numbers greater than 4,000 (for pipe flow) indicate turbulent flow.  The exact threshold can vary based on the geometry and specific conditions.

Reynolds Number Interpretation

• Laminar Flow (Re < 2,300)  -  Smooth and orderly, low Reynolds numbers, typically below 2,300. 
• Transitional Flow (2,300 < Re < 4,000)  -  Mixed laminar and turbulent, Reynolds numbers in the range of approximately 2,300 to 4,000.
• Turbulent Flow (Re > 4,000)  -  Chaotic and disorderly, high Reynolds numbers, generally above 4,000.

It's important to note that these Reynolds number ranges are general guidelines, and the transition from laminar to turbulent flow can be influenced by factors such as surface roughness, disturbances, and the specific geometry of the flow.  Engineers use these flow regimes to predict and analyze fluid behavior in various applications, including pipe flow, aerodynamics, and heat transfer.

Reynolds Number Formula
\( Re \;=\; \dfrac{\rho \cdot v \cdot l_c }{ \mu } \)     (Reynolds Number) \( \rho \;=\;  \dfrac{Re \cdot \mu }{ v \cdot l_c}   \)  \( v \;=\; \dfrac{Re \cdot \mu }{ \rho \cdot l_c } \)  \( l_c \;=\;   \dfrac{ Re \cdot \mu }{ \rho \cdot v }  \)  \( \mu \;=\; \dfrac {\rho \cdot v \cdot l_c }{ Re  } \)
Symbol	English	Metric
\( Re \) = Reynolds Number	\( dimensionless \)	\( dimensionless \)
\( \rho \)  (Greek symbol rho) = Fluid Density	\( lbm \;/\; ft^3 \)	\( kg \;/\; m^3 \)
\( v \) = Fluid Velocity	\( ft \;/\; sec \)	\( m \;/\; s \)
\( l_c \) = Characteristic Length or Diameter of Fluid Flow	\( in \)	\( mm \)
\( \mu \)  (Greek symbol mu)  = Fluid Dynamic Viscosity	\( lbf-sec \;/\; ft^2\)	\( Pa-s \)