Heat

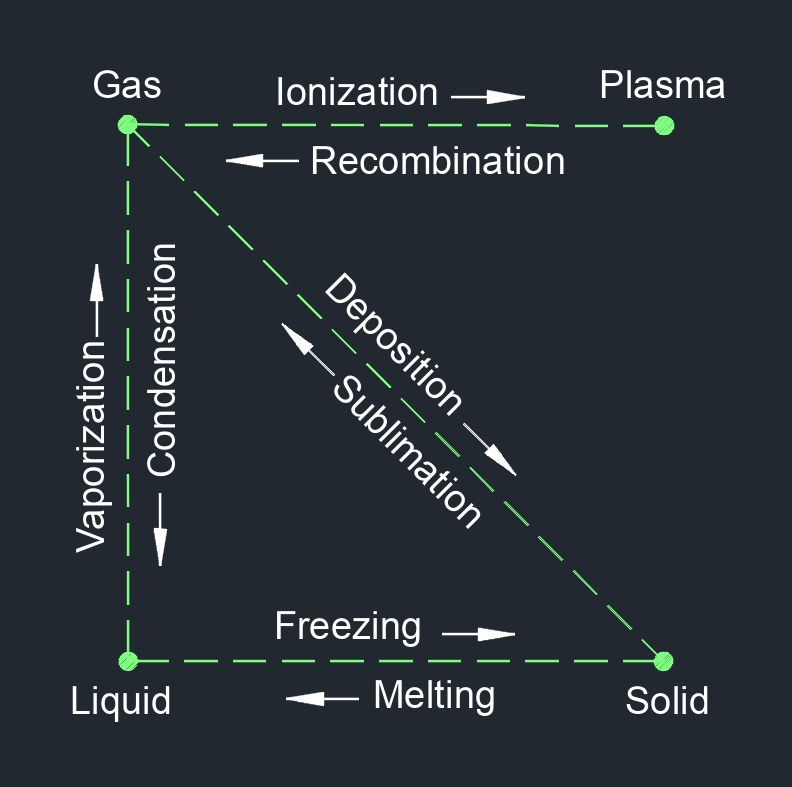Heat, abbreviated as q, (English unit \(\frac{Btu}{lbm}\), Metric unit \(\frac{kJ}{kg}\)), is a form of energy that causes physical change in what is being heated.  The lack of heat is cold.  This physical change comes from total amount of internal energy (kinetic energy and potential energy) possessed by an object or substance.  There is a basic difference between temperature and heat, heat is the amount of energy in a system.  The transfer of heat from higher or lower is because of the movement of molecules colliding, rotating, and vibrating into each other within a body.  When two objects come in contact with each other the thermal energy of the hotter object will be transfered to the colder object until both objects have the same thermal energy or temperature.

The Zeroth law of thermodynamics states when two thermal systems are in equilibrium and they with a third, then all are equal to each other.