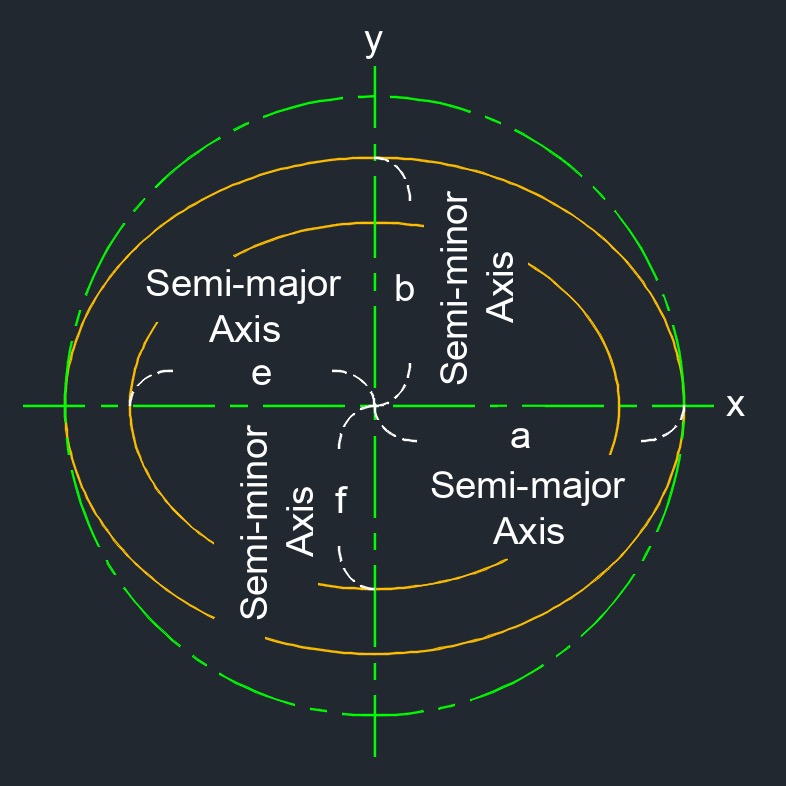
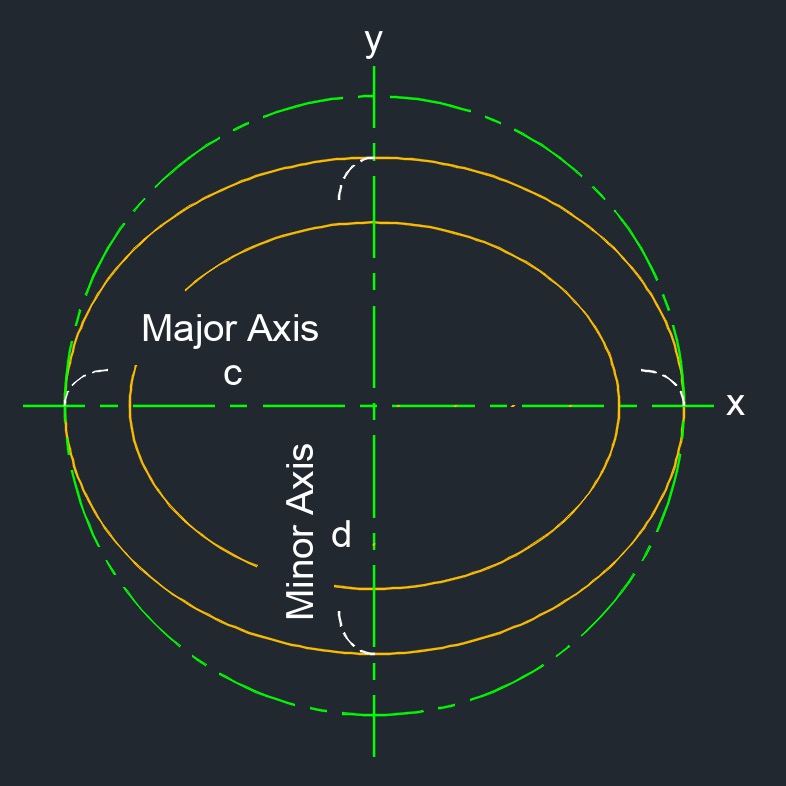
Area of a Hollow ellipse formula |
||
| \( A_{area} \;=\; \pi \cdot ( a \cdot b - e \cdot f ) \) | ||
| Symbol | English | Metric |
| \( A \) = area | \( in^2 \) | \( mm^2 \) |
| \( a \) = length semi-major axis | \( in \) | \( mm \) |
| \( b \) = length semi-minor axis | \( in \) | \( mm \) |
| \( e \) = length inner semi-major axis | \( in \) | \( mm \) |
| \( f \) = length inner semi-minor axis | \( in \) | \( mm \) |
| \( \pi \) = Pi | \(3.141 592 653 ...\) | \(3.141 592 653 ...\) |
- Hollow ellipse (a two-dimensional figure) has two ellipses with a conic section or a stretched circle.
- The major axis is always the longest axis in an ellipse.
- The minor axis is always the shortest axis in an ellipse.

Inner Semi-major Axis Length of a Hollow ellipse formula |
||
| \( e \;=\; a - g \) | ||
| Symbol | English | Metric |
| \( a \) = length semi-major axis | \( in \) | \( mm \) |
| \( b \) = length semi-minor axis | \( in \) | \( mm \) |
| \( g \) = ring width | \( in \) | \( mm \) |
Inner Semi-minor Axis Length of a Hollow ellipse formula |
||
| \( f \;=\; b - g \) | ||
| Symbol | English | Metric |
| \( a \) = length semi-major axis | \( in \) | \( mm \) |
| \( b \) = length semi-minor axis | \( in \) | \( mm \) |
| \( g \) = ring width | \( in \) | \( mm \) |