Compression Spring
Compression spring is a mechanical device designed to store and release mechanical energy. It is a type of helical spring, meaning it is made up of a tightly wound coil of wire with a constant diameter. Compression springs are widely used in various industries and applications. The primary function of a compression spring is to exert a force when it is compressed. When an external force is applied to the ends of the spring, it compresses and absorbs the energy, storing it within the spring. When the external force is released or removed, the spring expands and releases the stored energy, exerting a force in the opposite direction.
This property of compression springs makes them useful for a range of applications
- Suspension Systems - Compression springs are commonly used in vehicle suspension systems to absorb shocks and vibrations.
- Mechanical Devices - They are used in various mechanical devices to provide cushioning, dampening, and shock absorption.
- Industrial Equipment - Compression springs are employed in industrial machinery and equipment for tasks such as counterbalancing, clamping, and holding components together.
- Electrical Switches - They can be found in electrical switches to provide tension and ensure proper contact between the switch components.
- Consumer Products - Compression springs are utilized in numerous consumer products, such as pens, toys, and mattresses.
Compression springs are available in a wide range of sizes, materials, and designs to suit different requirements. The choice of material depends on factors such as desired strength, temperature resistance, corrosion resistance, and cost. Common materials used for compression springs include steel alloys, stainless steel, and various non-ferrous alloys. It's important to note that while compression springs are typically designed to operate in a linear fashion, they can also be designed for specific applications where they may have a non-linear force deflection characteristic or have other unique properties based on the design requirements.
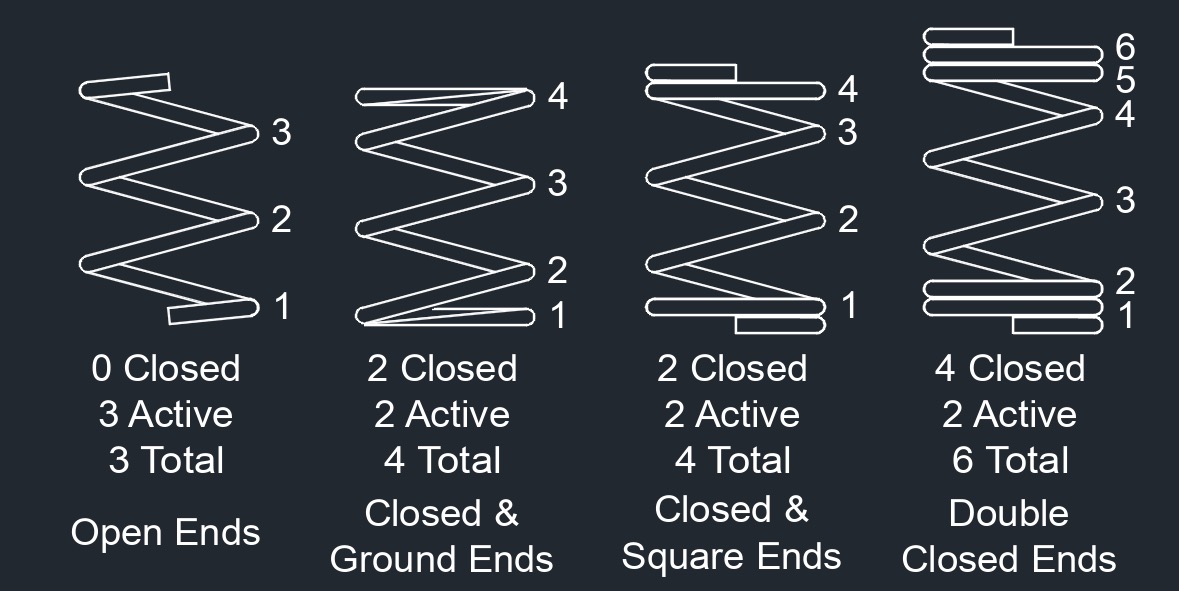
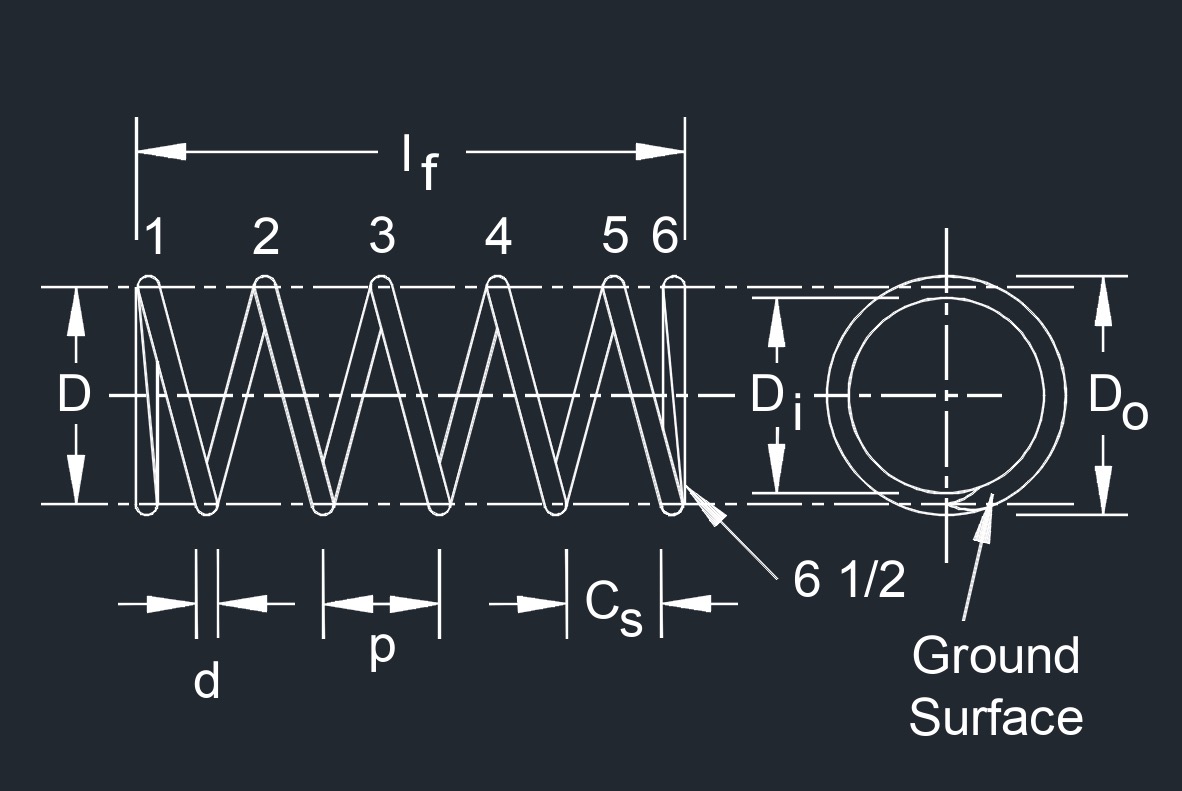

Tags: Strain and Stress Spring

