Square

on 29 January 2016. Posted in Plane Geometry

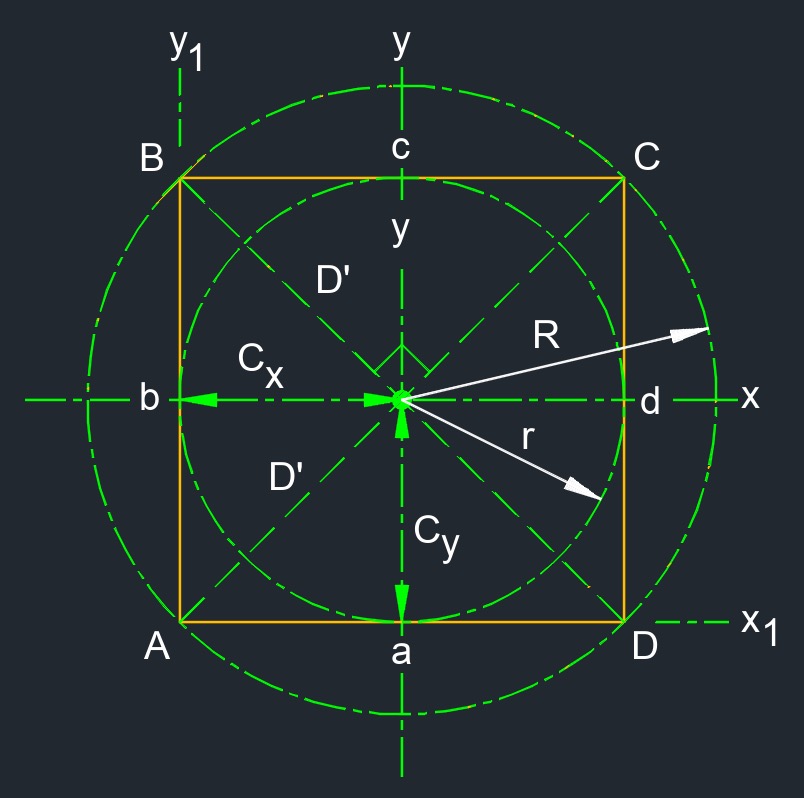Square (a two-dimensional figure) is a quadrilateral with four equal side lengths and 90° interior angles.
Abbreviated as SQ
Circumcircle is a circle that passes through all the vertices of a two-dimensional figure.
Diagonal is a line from one vertices to another that is non adjacent.
Inscribed circle is the largest circle possible that can fit on the inside of a two-dimensional figure.
Polygon (a two-dimensional figure) is a closed plane figure for which all edges are line segments and not necessarly congruent.
Quadrilateral (a two-dimensional figure) is a polygon with four sides.
a ∥ c
b ∥ d
a = b = c = d
∠A = ∠B = ∠C = ∠D = 360°
4 interior angles are 90°
2 diagonals
4 edges
4 vertex

Article Links

Area of a Square formulas
\( \large{ A_{area} = a^2 }\) \( \large{ A_{area} = \frac{D'^2}{2} }\) \( \large{ A_{area} = 4 \; r^2 }\) \( \large{ A_{area} = 2 \; R^2 }\)
Symbol	English	Metric
\(\large{ A_{area} }\) = area	\(\large{ in^2 }\)	\(\large{ mm^2 }\)
\(\large{ D' }\) = diagonal	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ a, b, c, d }\) = edge	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ r }\) = inside radius	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ R }\) = outside radius	\(\large{ in }\)	\(\large{ mm }\)

Circumcircle Radius of a Square formulas
\(\large{ R = \frac{a}{ \sqrt {2} } }\) \(\large{ R = \frac{D'}{2} }\)
Symbol	English	Metric
\(\large{ R }\) = outside radius	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ D' }\) = diagonal	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ a, b, c, d }\) = edge	\(\large{ in }\)	\(\large{ mm }\)

Diagonal of a Square formulas
\(\large{ D' = a \; \sqrt {2} }\) \(\large{ D' = \sqrt {2 \; A_{area} } }\) \(\large{ D' = 2 \; R }\) \(\large{ D' = 2 \; r \; \sqrt{2} }\) \(\large{ D' = 2\;R }\) \(\large{ D' = \frac{P}{ 2\; \sqrt{2} } }\)
Symbol	English	Metric
\(\large{ D' }\) = diagonal	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ A_{area} }\) = area	\(\large{ in^2 }\)	\(\large{ mm^2 }\)
\(\large{ a, b, c, d }\) = edge	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ r }\) = inside radius	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ R }\) = outside radius	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ P }\) = perimeter	\(\large{ in }\)	\(\large{ mm }\)

Distance from Centroid of a Square formulas
\(\large{ C_x = \frac { a } { 2 } }\) \(\large{ C_y = \frac { a } { 2} }\)
Symbol	English	Metric
\(\large{ C }\) = distance from centroid	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ a, b, c, d }\) = edge	\(\large{ in }\)	\(\large{ mm }\)

Elastic Section Modulus of a Square formulas
\(\large{ S = \frac { a^3 } { 6 } }\)
Symbol	English	Metric
\(\large{ S }\) = elastic section modulus	\(\large{in^3}\)	\(\large{mm^3}\)
\(\large{ a, b, c, d }\) = edge	\(\large{ in }\)	\(\large{ mm }\)

Inscribed Circle Radius of a Square formulas
\(\large{ r = \frac{a}{2} }\) \(\large{ r = \frac{P}{8} }\) \(\large{ r = \frac{D'}{2\; \sqrt{2} } }\) \(\large{ r = \frac{ \sqrt{A_{area} } }{2} }\) \(\large{ r = \frac{R}{ \sqrt{2} } }\)
Symbol	English	Metric
\(\large{ r }\) = inside radius	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ A_{area} }\) = area	\(\large{ in^2 }\)	\(\large{ mm^2 }\)
\(\large{ D' }\) = diagonal	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ a, b, c, d }\) = edge	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ R }\) = outside radius	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ P }\) = perimeter	\(\large{ in }\)	\(\large{ mm }\)

Perimeter of a Square formulas
\(\large{ P = 4\;a }\) \(\large{ P = 4\; \sqrt{A_{area} } }\) \(\large{ P = 2\;D'\; \sqrt{2} }\) \(\large{ P = 4\;R\; \sqrt{2} }\) \(\large{ P = 8\;r }\)
Symbol	English	Metric
\(\large{ P }\) = perimeter	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ A_{area} }\) = area	\(\large{ in^2 }\)	\(\large{ mm^2 }\)
\(\large{ D' }\) = diagonal	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ a, b, c, d }\) = edge	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ r }\) = inside radius	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ R }\) = outside radius	\(\large{ in }\)	\(\large{ mm }\)

Plastic Section Modulus of a Square formulas
\(\large{ Z = \frac{ a^3 }{ 4 } }\)
Symbol	English	Metric
\(\large{ Z }\) = plastic section modulus	\(\large{ in^3 }\)	\(\large{ mm^2 }\)
\(\large{ a, b, c, d }\) = edge	\(\large{ in }\)	\(\large{ mm }\)

Polar Moment of Inertia of a Square formulas
\(\large{ J_{z} = \frac {a^4}{6} }\) \(\large{ J_{z1} = \frac {2\;a^4}{3} }\)
Symbol	English	Metric
\(\large{ J }\) = torsional constant	\(\large{ in^4 }\)	\(\large{ mm^4 }\)
\(\large{ a, b, c, d }\) = edge	\(\large{ in }\)	\(\large{ mm }\)

Radius of Gyration of a Square formulas
\(\large{ k_{x} = \frac { a } { 2\; \sqrt 3 } }\) \(\large{ k_{y} = \frac { a } { 2\; \sqrt 3 } }\) \(\large{ k_{z} = \frac { a } { \sqrt 6 } }\) \(\large{ k_{x1} = \frac { a } { \sqrt 3 } }\) \(\large{ k_{y1} = \frac { a } { \sqrt 3 } }\) \(\large{ k_{z1} = \sqrt { \frac {2}{3} \;a } }\)
Symbol	English	Metric
\(\large{ k }\) = radius of gyration	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ a, b, c, d }\) = edge	\(\large{ in }\)	\(\large{ mm }\)

Second Moment of Area of a Square formulas
\(\large{ I_{x} = \frac {a^4}{12} }\) \(\large{ I_{y} = \frac {a^4}{12} }\) \(\large{ I_{x1} = \frac {a^4}{3} }\) \(\large{ I_{y1} = \frac {a^4}{3} }\)
Symbol	English	Metric
\(\large{ I }\) = moment of inertia	\(\large{ in^4 }\)	\(\large{ mm^4 }\)
\(\large{ a, b, c, d }\) = edge	\(\large{ in }\)	\(\large{ mm }\)

Radius of Gyration of a Square formulas
\(\large{ J = 2.25 \; \left( \frac { a } { 2 } \right) ^4 }\)
Symbol	English	Metric
\(\large{ J }\) = torsional constant	\(\large{ in^4 }\)	\(\large{ }mm^4\)
\(\large{ a, b, c, d }\) = edge	\(\large{ in }\)	\(\large{ mm }\)

Piping Designer Logo 1