Area Cross-section

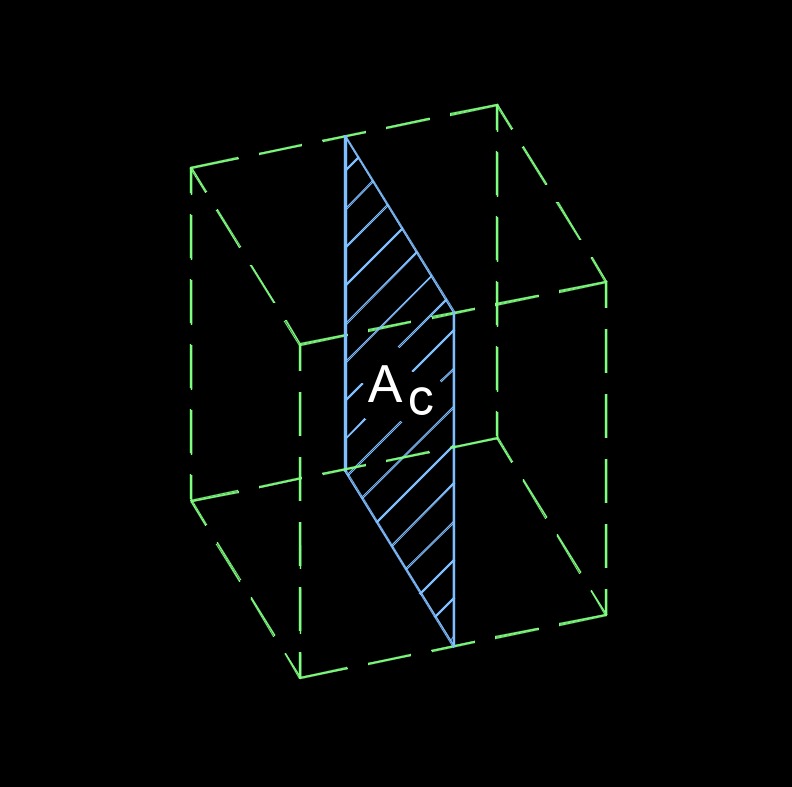
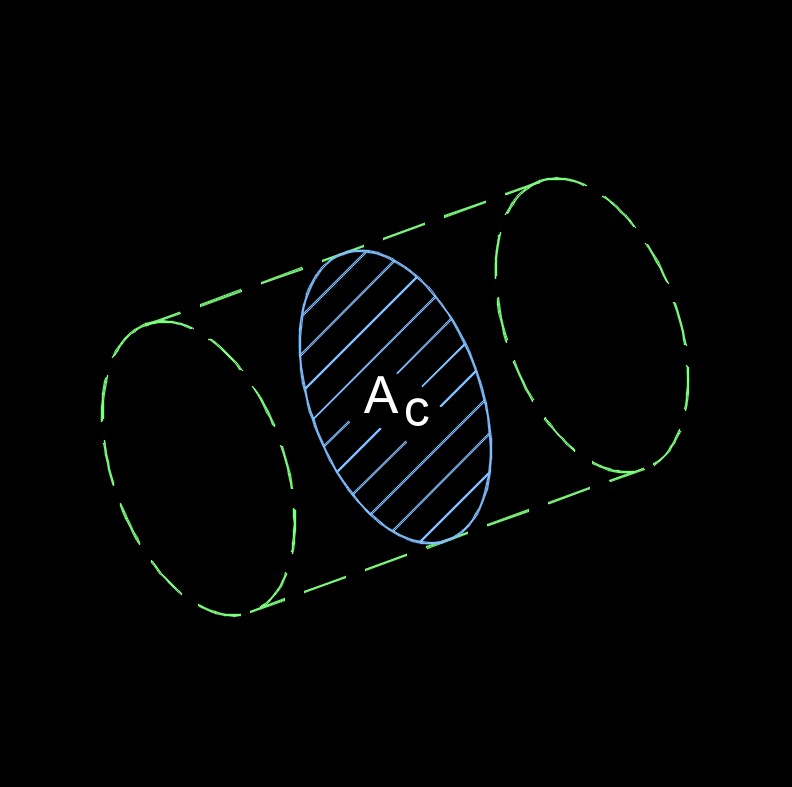Area cross-section, abbreviated as \(A_c\), is a two-dimension slice of a plane that is perpendicular to its axis of a three-dimension plane.  In engineering and physics, area cross-section is often used to calculate flow rates, forces, and other parameters in fluid and gas systems.  

Area cross-section can be calculated using a variety of mathematical formulas, depending on the shape of the object.  In many cases, the area cross-section can be approximated using simple geometric shapes, such as circles or rectangles, while in other cases, more complex mathematical models may be required.

For example, in a pipe or duct, the area cross-section is the area of the circular or rectangular opening of the pipe or duct.  The area cross-section of a pipe or duct is an important parameter for determining the flow rate of the fluid or gas flowing through it, as well as the pressure drop across the pipe or duct.