Moment of Inertia of a Sphere

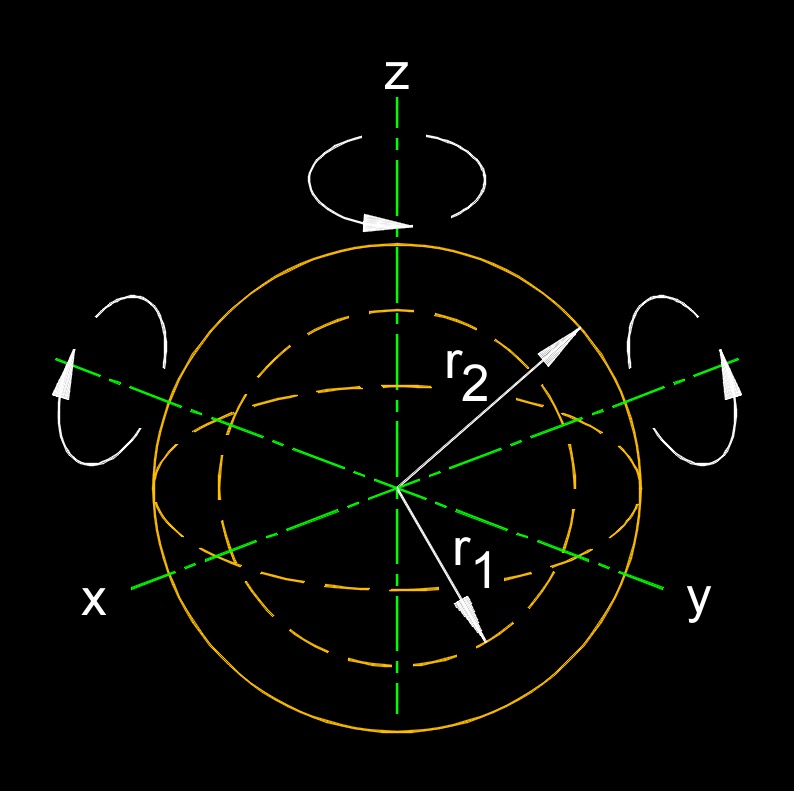
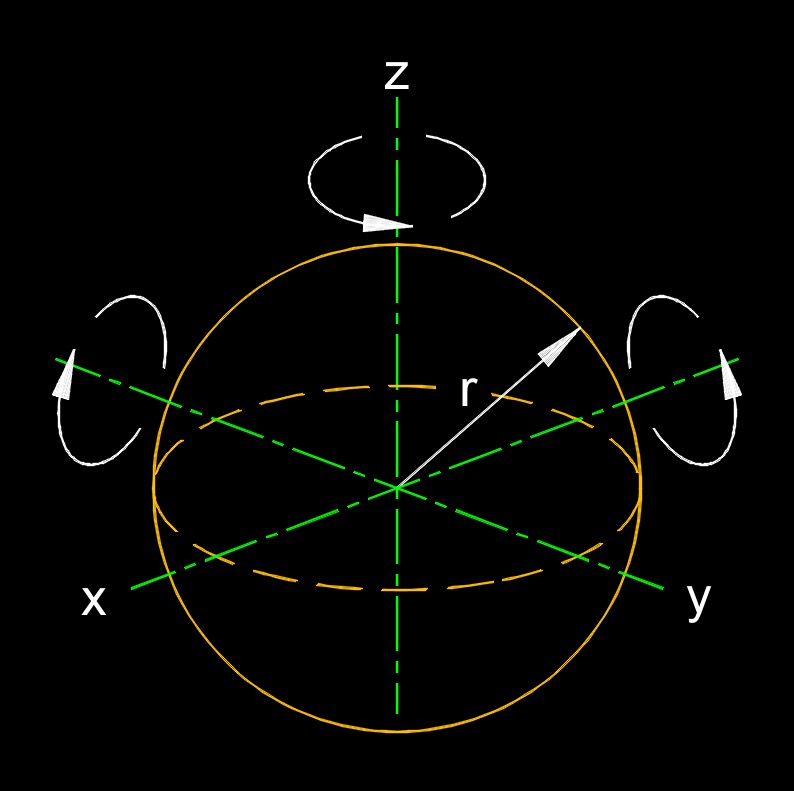This calculation is for the moment of inertia of a sphere.  There are three separate calculations:  a solid sphere, a hollow sphere and a hollow core sphere.  The difference between a hollow sphere and a hollow core sphere is a hollow sphere has a thin shell, or a thickness that is neglible.  Because a sphere is the same dimensions in every dimension, the moment of inertia is the same about every axis.

 

Artical Links

•  Sphere

 

 

Moment of Inertia of a Sphere Formula, Solid Sphere
\(\large{ I = \frac {2}{5} \; m \; r^2 }\)
Symbol	English	Metric
\(\large{ I }\) = moment of inertia	\(\large{\frac{lbm}{ft^2-sec}}\)	\(\large{\frac{kg}{m^2}}\)
\(\large{ m }\) = mass	\(\large{ lbm }\)	\(\large{ kg }\)
\(\large{ r }\) = radius	\(\large{ in }\)	\(\large{ mm }\)

 

Moment of Inertia of a Sphere Formula, Hollow Sphere
\(\large{ I = \frac {2}{3} \; m \; r^2 }\)
Symbol	English	Metric
\(\large{ I }\) = moment of inertia	\(\large{\frac{lbm}{ft^2-sec}}\)	\(\large{\frac{kg}{m^2}}\)
\(\large{ m }\) = mass	\(\large{ lbm }\)	\(\large{ kg }\)
\(\large{ r }\) = radius	\(\large{ in }\)	\(\large{ mm }\)

 

Moment of Inertia of a Sphere Formula, Hollow Core Sphere
\(\large{ I = \frac {2}{5} \; m \; \left( \frac { r_2^5 \;-\; r_1{^5} } { r_2{^3} \;-\; r_1{^3} }  \right)    }\)
Symbol	English	Metric
\(\large{ I }\) = moment of inertia	\(\large{\frac{lbm}{ft^2-sec}}\)	\(\large{\frac{kg}{m^2}}\)
\(\large{ m }\) = mass	\(\large{ lbm }\)	\(\large{ kg }\)
\(\large{ r }\) = radius	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ r_1 }\) = radius	\(\large{ in }\)	\(\large{ mm }\)
\(\large{ r_2 }\) = radius	\(\large{ in }\)	\(\large{ mm }\)

 

Moment of Inertia of a Sphere Calculator