Friction

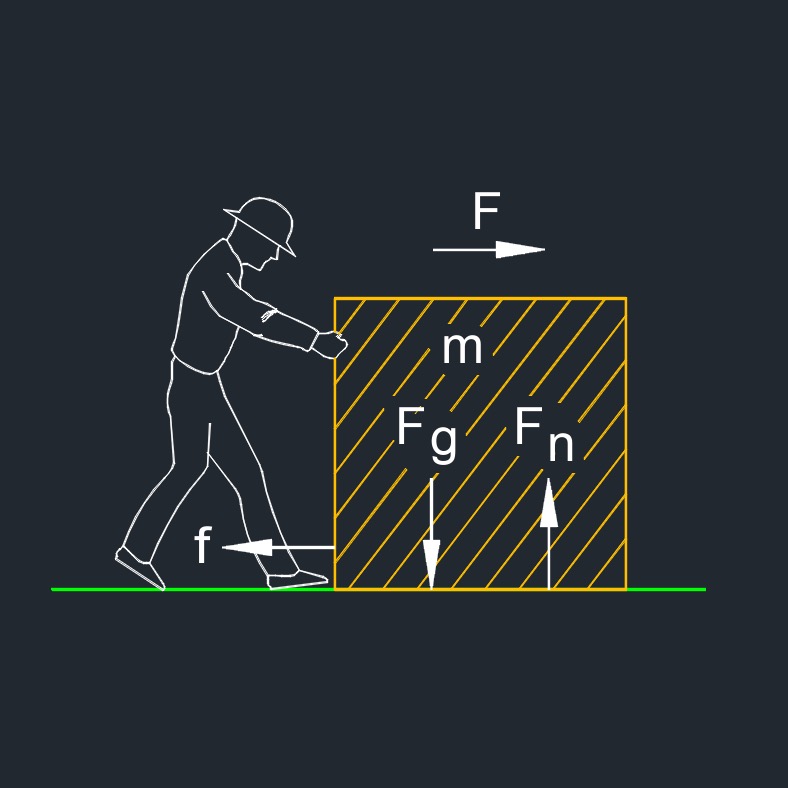Friction, abbreviated as f, also called force of friction, is the mechanical resistance to the relative movement of two surfaces.  The frictional force on each body is in an opposite direcrion to the motion of the other body.  Since no surface is perfectly smooth, all having at least a minute roughness, there will always be friction, no matter how small the friction.

Friction is a force that opposes the relative motion or tendency of motion between two surfaces in contact.  It occurs when there is an attempt to move one surface past another or when there is an actual motion between the surfaces.  Friction acts parallel to the interface of the surfaces and can impede or resist the motion.

Friction arises due to the microscopic irregularities on the surfaces in contact.  As the surfaces slide or try to slide past each other, these irregularities interlock and create resistance, leading to the generation of frictional forces.  The magnitude of friction depends on several factors, including the nature of the surfaces in contact, the normal force pressing the surfaces together, and the roughness or smoothness of the surfaces. 

It is also influenced by external factors such as temperature and the presence of lubricants.  Friction has both advantages and disadvantages.  On one hand, it allows us to walk, grip objects, and control the motion of vehicles.  On the other hand, it can cause energy losses, wear and tear of surfaces, and inefficiencies in mechanical systems.  Therefore, understanding and managing friction is crucial in various fields, including engineering, physics, and everyday life.

Friction Formula
\( f \;=\; \mu \; F_n \)     (Friction) \( \mu \;=\; f \;/\; F_n \) \( F_n \;=\; f \;/\; \mu \)
Symbol	English	Metric
\( f \) = Friction	\( lbf \)	\(N\)
\( \mu \)  (Greek symbol mu) = Friction Coefficient	\( dimensionless \)	\( dimensionless \)
\( F_n \) = Normal Force	\( lbf \)	\(N\)

Friction Types

Friction is when two objects in contact with each other resist movement or slows down.

External Friction  -  Forces caused by external agent present outside of the system.  External non-zero net force imparts an acceleration to the center of mass of the system regardless of point of application.

• Dry Friction  -  The resistive force between solid surfaces in contact that resists their relative tangential motion.
• Dynamic Friction (types are fluid, kinetic, and rolling friction)  -  Is resistance to relative movement of two bodies that are already in motion and rubing togeather.
• Kinetic Friction  -  When two surfaces in contact are in relative motion (one surface slides across another).
• Rolling Friction  -  Weaker than kinetic (sliding) or static friction, this one acts on objects when they are rolling over a surface.
• Sliding Friction (also called dynamic friction or kinetic friction)  -  Resistance to relative movement of two bodies that are already in motion and rubing togeather.
• Static Friction -  When two objects in contact are not in relative motion (one surface stationary, the other slides across).

Internal Friction  -  Forces exchanged by the objects in the system.  The force resisting motion between the elements making up a solid material while it undergoes deformation.  This can be due to either or both an applied force or the change in temperature.

• Fluid Friction (Viscous Friction)  -  Includes gasses and liquids, acts on objects when they are moving through fluid relative to each other.  The force exerted on an object depends on the material, shape of, speed, and viscosity of the liquids.
• Temperature change  -  Temperature does not effect the friction coefficient, for either kinetic or static.

• Friction is proportional and perpendicular to normal loads for any object under motion.

• The surface characteristics an object comes in contact with determines the friction between them.

• For any two objects moving across each other, the area of contact surface does not influence the frictional force between them.

• The kinetic friction between two dry objects is independent of the relative surface velocity.

• The static friction coefficient is more than the kinetic friction coefficient.

Laws of Kinetic Friction

• The force of friction always acts in the opposite direction in which the body is moving between two surfaces in contact.

• The force of kinetic friction is independent of shape and area of the surfaces in contact.

• The magnitude of the kinetic friction bears a constant ratio to the normal reaction between the two surfaces.

• For moderate speeds, the force of friction remains constant.  But it decreases slightly with the increase in speed.

• The kinetic friction coefficient is less than the static friction coefficient.

Laws of Static Friction

• The force of friction that is trying to oppose the movement of a stationary object.

• The force of friction always acts in a direction opposite to that in which the body tends to move.

• The magnitude of the force of friction is equal to the force which tends the body to move.

• The force of friction is independent of the area of contact between the two surfaces.

• The force of friction depends upon the roughness of the surfaces.

• The static friction coefficient is more than the kinetic friction coefficient.