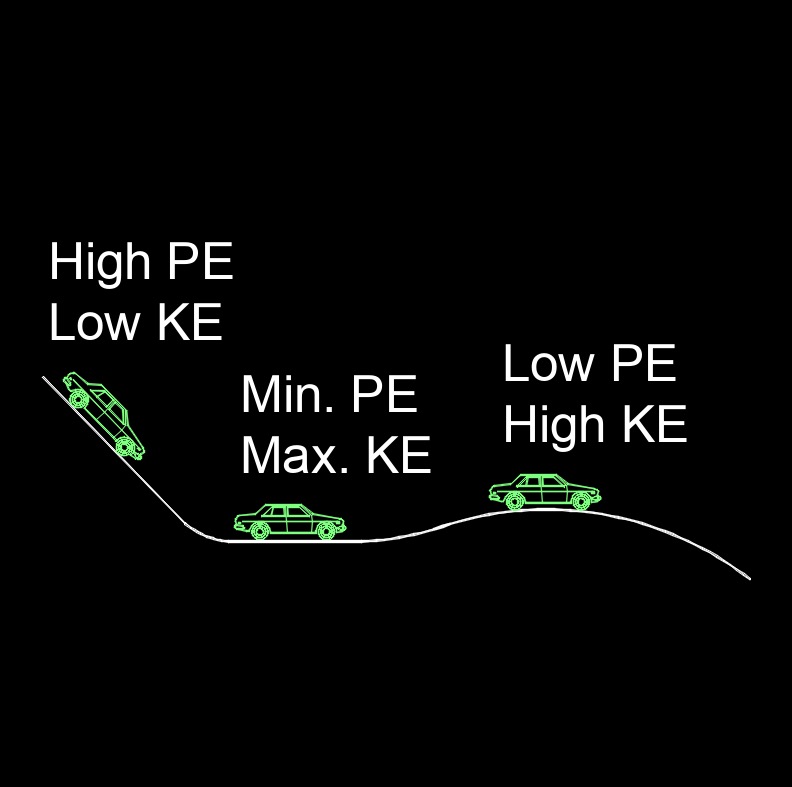
Kinetic energy, abbreviated as KE, is the energy an object possesses by virtue of its motion. It is a scalar quantity and is dependent on the mass and speed of the object. If it moves, it has kinetic energy. The energy an object possesses due to its motion. Kinetic energy is a scalar quantity, meaning it has only magnitude and no direction. It is a type of mechanical energy, which is the sum of kinetic and potential energy in a system.
- See Articles Kinetic Energy Types - Electric Energy / Electromagnetic Energy / Geothermal Energy / Impact Energy / Internal Energy / Mechanical Energy / Radiant Energy / Sound Energy / Thermal Energy / Tidal Water Energy / Wind Energy
Kinetic Energy Formula |
||
|
\( KE \;=\; \frac{ 1 }{ 2} \cdot m \cdot v^2 \) (Kinetic Energy) \( m \;=\; \dfrac{ 2 \cdot KE }{ v^2 } \) \( v \;=\; \sqrt{ \dfrac{ 2 \cdot KE }{ m } } \) |
||
| Symbol | English | Metric |
| \( KE \) = Kinetic Energy | \( lbf-ft \) | \(J\) |
| \( m \) = Mass | \(lbm\) | \(kg\) |
| \( v \) = Velocity | \(ft \;/\; sec\) | \(m \;/\; s\) |
