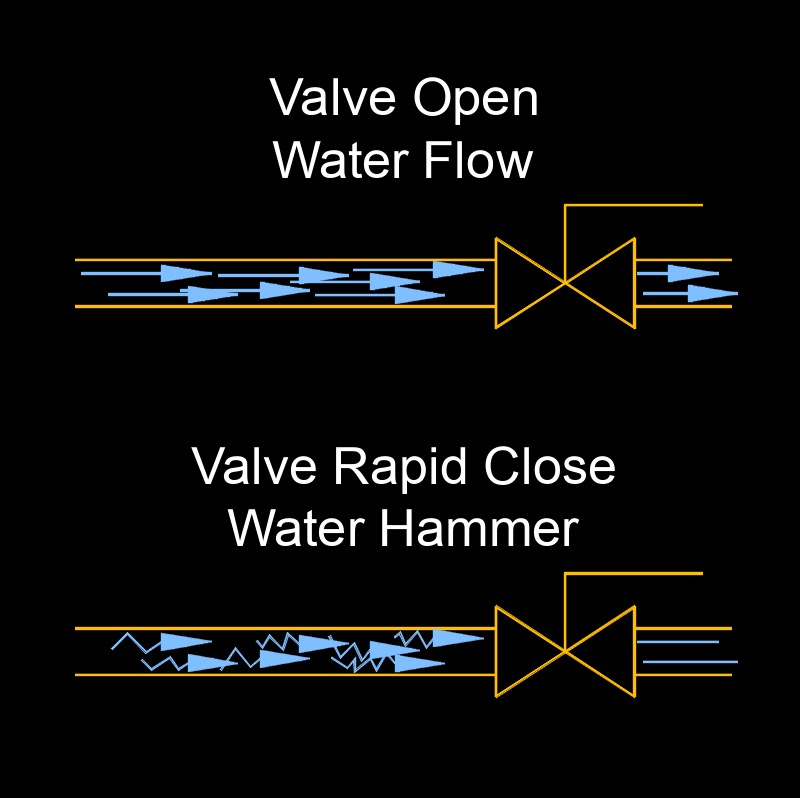
Water hammer, abbreviated as WH, also called hydraulic shock, surge pressure or fluid hammer, is a phenomenon that occurs in fluid dynamics when there is a sudden change in the flow of a liquid, such as water, in a closed piping system. It is characterized by a sharp, banging or hammering noise and can result in significant pressure fluctuations within the system.
Water Hammer Happens When
Sudden Valve Closure - One of the most common causes of water hammer is the abrupt closure of a valve in the
pipeline. When a
valve is closed quickly, the moving fluid is suddenly stopped, causing a rapid increase in pressure in the
pipe. This increased pressure can create shock waves that travel through the system, leading to the characteristic banging noise and potential damage.
Pump Start/Stop - Another scenario is when a pump is started or stopped suddenly. If a pump is turned on rapidly, it can create a surge of water that travels through the piping system, potentially causing water hammer. Similarly, when a
pump is shut off abruptly, the
momentum of the flowing water can lead to pressure spikes.
Changes in Flow Direction - Changes in flow direction, such as sharp bends or tees in the pipeline, can also contribute to water hammer. These changes can cause the fluid to change direction suddenly, resulting in pressure fluctuations.
Air in the System - The presence of air pockets or bubbles in the piping system can exacerbate water hammer because air compresses and can act as a cushion, absorbing some of the shock. When these air pockets collapse, they can intensify the pressure spikes.
Water Hammer can have Various Negative Effects
- Potential damage to pipes, valves, and fittings due to the high-pressure spikes.
- Noise pollution from the banging or hammering sound, which can be quite loud and disruptive.
- Reduced system efficiency and reliability.
- Increased risk of leaks and component failure over time.
To mitigate water hammer, engineers often use various methods, including the installation of surge suppressors, gradual valve closures, and proper system design to minimize sudden changes in flow velocity. Additionally, maintaining and venting air from the system can help reduce the severity of water hammer events.
