Temperature Difference Formula |
||
| \( \Delta T \;=\; T_f - T_i \) | ||
| Symbol | English | Metric |
| \( \Delta T \) = Temperature Difference | \( F \) | \( K \) |
| \( T_f \) = Final Temperature | \( F \) | \( K \) |
| \( T_i \) = Initial Temperature | \( F \) | \( K \) |
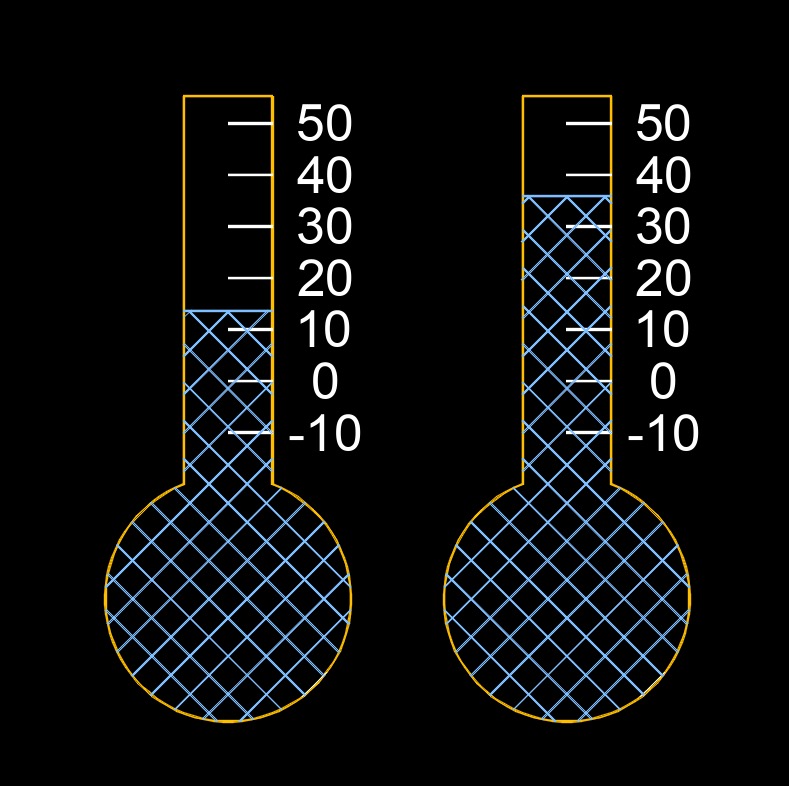 Temperature difference, abbreviated as \(\Delta T\) or TD, is the difference between two specific temperature points of a volume at a given time in a system.
Temperature difference, abbreviated as \(\Delta T\) or TD, is the difference between two specific temperature points of a volume at a given time in a system.
