Torsion Spring

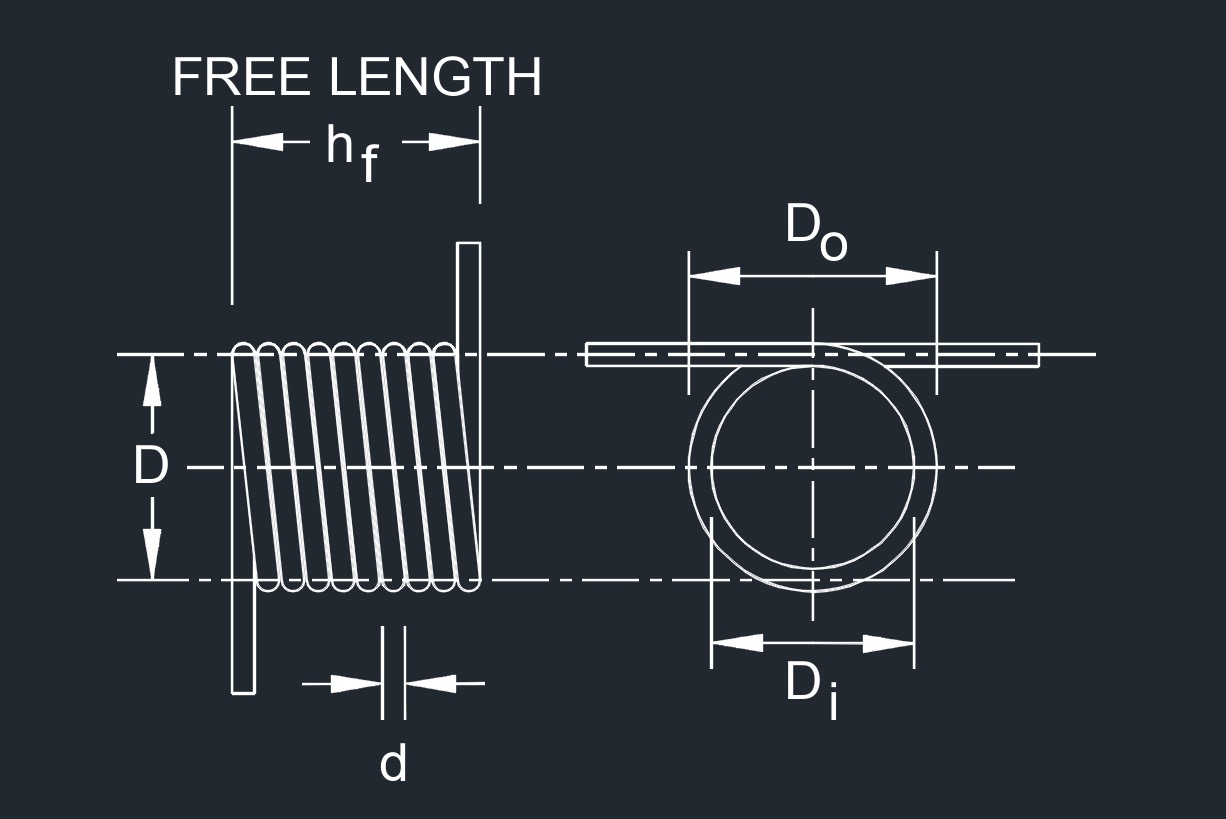
A torsion spring works by twisting or exerting torque along its axis.  It stores mechanical energy when twisted and releases it when the twisting force is removed.  Torsion springs are commonly used in various applications to provide resistance to rotational or torsional forces.  Compression springs and extension springs work with pulling and pushing forces, but tortion springs work with twisting forces.  After being twisted a porportional force to the applied force is exerted in the opposite direction.  The ends of the spring are attached to other components and rotated around the spring center as the spring pushes back to its origional position.

Key Points about Torsion Springs

Helical Shape  -  Torsion springs are typically coiled into a helical shape, resembling a tightly wound spiral.  The coiled design allows them to store and release energy efficiently.
Torque Generation  -  When a torsion spring is twisted or rotated about its axis, it generates a torque or twisting force.  This torque can be used to bring objects back to their original positions when the twisting force is removed.
Wire Diameter and Material  -  Torsion springs are usually made from round wire with a consistent diameter.  The choice of material depends on the specific application and desired properties, such as flexibility, strength, and corrosion resistance.  Common materials include steel, stainless steel, and various alloys.
Ends and Attachments  -  Torsion springs have different types of ends or attachments to allow them to be connected to other components or mounted in a device.  Common types of ends include straight ends, hooked ends, or custom designed attachments.
Direction of Wind  -  Torsion springs can be designed with either a left hand or right hand wind, depending on the application's requirements.  The direction of wind determines the direction of the torque generated when the spring is twisted.

Torsion springs are used in a wide range of applications, including garage doors, automotive suspension systems, industrial machinery, and various mechanical devices that require rotational or twisting force control.  They provide a compact and efficient means of storing and releasing energy in such systems.  The design and specifications of a torsion spring are carefully engineered to meet the specific needs of each application.