Angular Acceleration

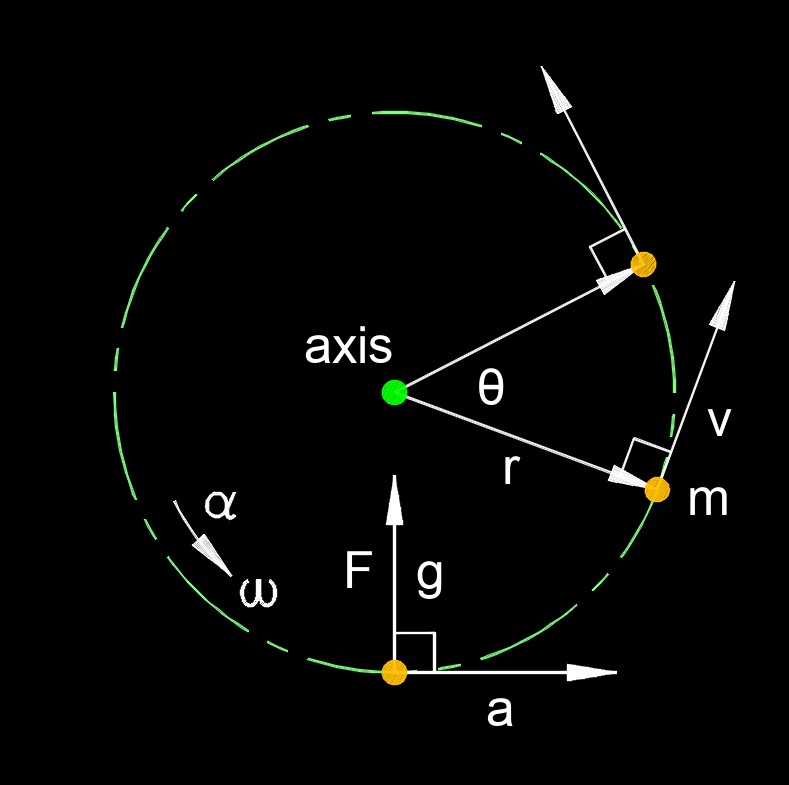Angular acceleration, abbreviated as \(\alpha\) (Greek symbol alpha), also called rotational acceleration, is the rate at which the angular velocity of an object changes over time.  It represents how quickly an object's rotational speed or direction of rotation is changing. 

The sign of angular acceleration indicates whether the rotational motion is speeding up or slowing down.  A positive angular acceleration indicates an increase in the angular velocity, causing the object to rotate faster.  Conversely, a negative angular acceleration represents a decrease in the angular velocity, resulting in a slower rotation.  Zero angular acceleration means that there is no change in the angular velocity, indicating a constant rotational speed.

Angular acceleration is a used in rotational dynamics and plays a crucial role in analyzing the behavior of rotating objects.  It is used to describe the acceleration of rotating systems, such as spinning tops, wheels, or rotating machinery.  Understanding angular acceleration is important for various applications, including the design and analysis of mechanical systems, robotics, gyroscopic stabilization, and celestial mechanics.  It enables engineers and scientists to predict and control the rotational behavior of objects, determine the forces and torques involved, and optimize the performance of rotational systems.

 

Angular acceleration formula
\( \alpha \;=\; \Delta \omega \;/\; \Delta t  \)     (Angular Acceleration) \( \Delta \omega \;=\; \alpha \; \Delta t    \) \( \Delta t \;=\; \Delta \omega \;/\; \alpha  \)
Symbol	English	Metric
\( \alpha \)  (Greek symbol alpha) = Angular Acceleration	\(deg \;/\; sec^2\)	\(rad \;/\; s^2\)
\( \Delta \omega \)  (Greek symbol omega) = Average Angular Velocity	\(deg \;/\; sec\)	\(rad \;/\; s\)
\( \Delta t \) = Average Time	\( sec \)	\( s \)