Centripetal Acceleration

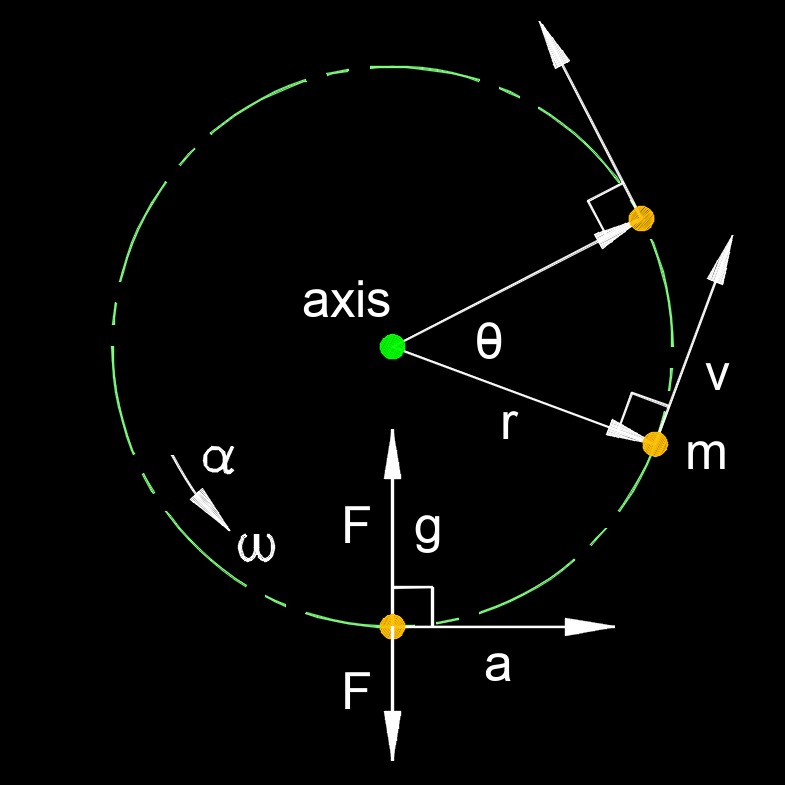Centripetal acceleration, abbreviated as \( a_c \), is the acceleration directed towards the center of a circular path that an object follows when it is in uniform circular motion.  In other words, it is the acceleration that keeps an object moving in a circular path instead of a straight line.  Centripetal acceleration is always directed inward, toward the center of the circle, and its magnitude depends on the object's speed and the radius of the circular path.  This formula tells us that the greater the speed of the object or the smaller the radius of the circle, the greater the centripetal acceleration required to keep it in circular motion.

Centripetal acceleration is essential in various real world scenarios, such as the motion of planets around the sun, cars navigating curves on a road, or a spinning object on a string.  It's important to note that centripetal acceleration does not represent a change in speed (as it is perpendicular to the velocity vector), but rather a change in the direction of motion, allowing the object to maintain a curved path.

 

Centripetal acceleration formula
\( a_c \;=\;   v^2 \;/\; r \)     (Centripetal Acceleration) \( v \;=\; \sqrt{ a_c \; r }   \) \( r \;=\; v^2 \;/\; a_c \)
Symbol	English	Metric
\( a_c \) = Centripetal Acceleration	\(ft \;/\;sec^2\)	\(m \;/\;s^2\)
\( r \) = Radius	\(ft\)	\(m\)
\( v \) = Velocity	\(ft \;/\; sec\)	\(m \;/\;s\)

 

Centripetal acceleration formula
\( a_c \;=\; \omega^2 \; r  \)     (Centripetal Acceleration) \( \omega \;=\; \sqrt{  a_c \;/\; r   }  \) \( r \;=\; a_c \;/\; \omega^2 \)
Symbol	English	Metric
\( a_c \) = Centripetal Acceleration	\(ft \;/\; sec^2\)	\(m \;/\;s^2\)
\( \omega \)  (Greek symbol omega) = Angular Velocity	\(ft \;/\;sec\)	\(m \;/\;s\)
\( r \) = Radius	\(ft\)	\(m\)