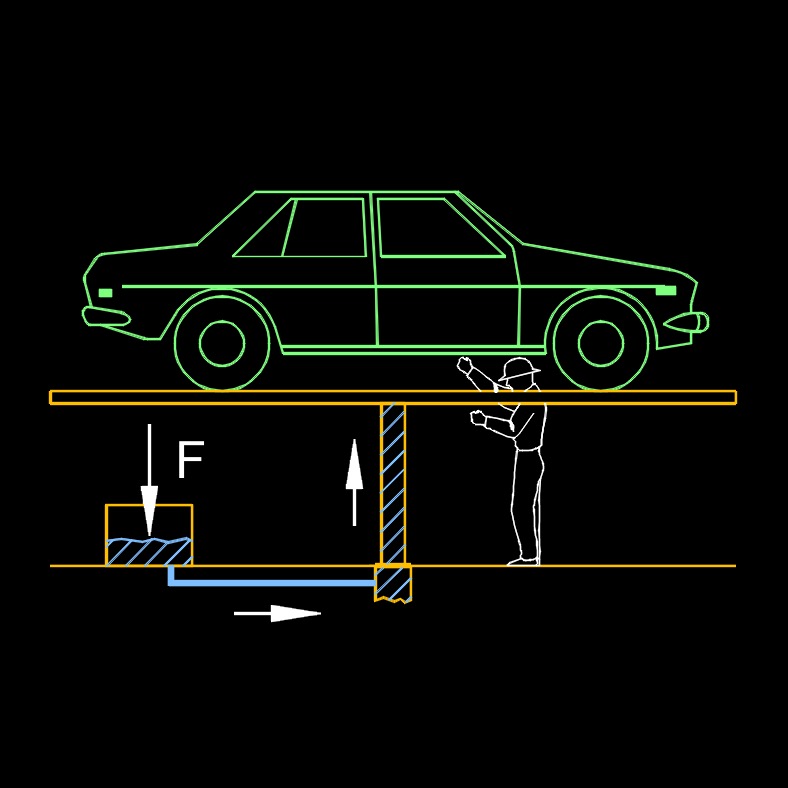Hydraulics is the force or motion applied on a confined liquid. A incompresible fluid is used to applying presure at the smaller end, it will have the same pressure applied to the other end which is large in diameter. It involves the use of pressurized fluids to generate, control, and transmit power. Hydraulic systems utilize the principles of fluid dynamics to generate and transmit forces and motion. They typically involve the use of a liquid, such as oil or water, which is confined within a system of pipes, cylinders, valves, and actuators. By applying pressure to the fluid, hydraulic systems can transmit this force and motion to various mechanical components, allowing for the control and operation of machinery and equipment.
Hydraulics find applications in various industries, including automotive, construction, manufacturing, aerospace, and agriculture. They are used in systems such as hydraulic brakes, hydraulic lifts, hydraulic presses, excavators, cranes, steering systems, and aircraft landing gear, among others. Hydraulic systems offer advantages such as high power density, precise control, safety, and versatility.
Understanding the principles of hydraulics and the behavior of hydraulic systems is essential for engineers and technicians involved in the design, operation, and maintenance of hydraulic machinery and equipment.
- See Articles - List of Tags, List of Categories, List of Articles, List of Glossaries, Nomenclature and Symbols, (See Hydraulic Glossary)
Hydraulic Systems
Aviation Hydraulic System - These draw fluid from a reservoir and apply pressure to give to other components. It then returns the fluid to the reservoir.
Closed-loop System - When the pump operates there will be pressure for fluids. The fluid will flow continuously between the pump and the actuator without entering into the reservoir for a closed loop system.
Fixed Displacement System - A system in which the amount of displacement that the pump produces cannot be changed.
Hydraulic Motors and Cylinders System - A basic hydraulic system has motors and cylinders that utilize pressurized fluid for mechanical work. Hydraulic motors convert pressure into torque and rotation or displacement. The various types of these motors include vane, radial piston, and gear.
Hydraulic Pump System - Hydraulic system components are driven by a variety of power sources. The different types of pumps are gear pumps, fixed displacement piston pumps, and variable displacement piston pumps.
Open-loop System - When the actuating mechanism is idle, there will be fluid flow but no pressure.
How Hydraulic Systems Work
Hydraulic system depends on the pressure applied on the hydraulic fluid which creates power used for performing different tasks. The force applied on fluid at one point gets transmitted through the connected components and enables some other point required for working. The fluid which may be water, petrol or other liquid when pressurized acts on every part of the vessel creating power which is capable of lifting heavy loads.
Hydraulic Uses
Airplane Hydraulic System - Hydraulics is applied in airplanes and jet planes in many instances like adjusting wings, retraction and extension of landing gears, opening/closing of doors, brakes, steering, etc.
Hydraulic Brake - Braking system of the vehicle is an important example of hydraulics. They are classified based on frictional contact mechanism(drum brake and disk brake) and brake force distribution(single acting and double acting).
Hydraulics Equipment - Hudraulic based heavy equipment will have more strength and ability to move quickly.
Hydraulic Jack - They are strong and can lift heavy loads. A hydraulic jack comprises of a cylinder and pumping system for storing and transferring hydraulic fluid.
Hydraulic Lift - Used for moving goods or people vertically. When the pressure is applied to the liquid, the force transmits to all the points of the container.
Hydraulic Power Steering - An important part of the vehicles that help to change the direction of the vehicle to left or right. This system reduces the effort of drivers and absorbs road shocks.
Hydraulic Shock Absorbers - A device used to absorb and damp shock impulses. A cylinder with hydraulic oil and a piston are the components used for developing shock absorber.
Hydraulic Pumps
Air Pump - Air hydraulic pumps use compressed air to stimulate a pump mechanism, generating useful energy from a pressurized liquid. These devices are also known as pneumatic hydraulic pumps and are applied in a variety of industries to assist in the lifting of heavy loads and transportation of materials with minimal initial force.
Clutch Pump - This is a small displacement gear pump equipped with a belt-driven, electromagnetic clutch, much like that found on a car’s air conditioner compressor. It is engaged when the operator turns on a switch inside the truck cab. Clutch pumps are frequently used where a transmission power take-off aperture is not provided or is not easily accessible. Common applications include aerial bucket trucks, wreckers and hay spikes. As a general rule clutch pumps cannot be used where pump output flows are in excess of 15 GPM as the engine drive belt is subject to slipping under higher loads.
Dump Pump - This type of pump is commonly used in dumping applications from dump trailers to tandem axle dump trucks. The dump pump is specifically designed for one application, dump trucks, and is not suitable for other common trailer applications such as live floor and ejector trailers.
Electric Pump - This pump use electricity to operate. They are frequently used to transfer hydraulic liquid from a reservoir to an actuator, like a hydraulic cylinder.
Gear Pump - Gear pumps operate by compressing fluid between the inside wall of the gear housing and the trapped air volume of the meshing gear teeth. They are usually classified as internal or external, with internal gear pumps being the more reliable of the two. In addition, internal gear pumps can dry run for short periods. This design is characterized as having fewer moving parts, being easy to service, more tolerant of contamination than other designs and relatively inexpensive. Gear pumps are fixed displacement, also called positive displacement, pumps. This means the same volume of flow is produced with each rotation of the pump’s shaft.
Hand Pump - Hydraulic hand pumps are used for fluid transmission that utilize the mechanical force generated by a manually operated actuator. A manually operated actuator could be a lever, a toggle, a handle, or any of a variety of other parts.
Piston Pump - Piston pumps are a bit more complex and can achieve much higher levels of pressure than either vane or gear pumps. They are the pumps you will use in high pressure applications. A piston pump is a positive displacement pump that uses a high pressure seal working reciprocally with a piston to move fluid. This configuration allows them to operate under high pressure without noticeably affecting flow rate.
Vane Pump - In a vane pump, rotors with slots are mounted to a shaft that spins eccentrically to a cam ring, thus creating vane chambers. The vane chambers on the discharge side decrease in volume and force fluid out, those on the intake side increase in volume and draw fluid in. Vane pumps were at one time commonly used on utility vehicles such as aerial buckets and ladders. Today, the vane pump is not commonly found on these mobile hydraulic systems as gear pumps are more widely accepted and available.
Hydraulic Valves
Directional Control Valve - Used to route hydraulic fluid in a system to various devices as needed. They shift between discrete positions such as extend, retract, or neutral position for controlling a hydraulic cylinder. They are also capable of shifting into intermediate positions wherein they can be used to control the speed, direction, or acceleration of an actuator.
Flow Control Valve - Used to adjust the flow rate of hydraulic fluid in a hydraulic system. These valves have a port that is able to be adjusted so that the flow area may be changed to provide an alteration in the flow rate through the valve. The speed of motion of these valves are a direct function of flow rate, reducing the flow rate reduces the speed of their operation and vice versa.
Pressure Control Valve - Used to regulate the fluid pressure that is passing through hydraulic systems to maintain that pressure at desired levels in the system. Fluid systems are typically designed for operation at a set range of pressures. These valves serve to prevent rises in pressure that may result in leaks of hydraulic fluid or the bursting of pipes and tubing. They are also used to maintain a set pressure in a part of a hydraulic circuit.
