Cavitation number formula |
||
|
\( Ca \;=\; \dfrac{ p - p_v }{ \dfrac{1}{2} \cdot \rho \cdot v^2 }\) (Cavitation Number) \( p \;=\; \dfrac{1}{2} \cdot Ca \cdot \rho \cdot v^2 + p_v \) \( p_v \;=\; p - \dfrac{1}{2} \cdot Ca \cdot \rho \cdot v^2 \) \( \rho \;=\; \dfrac{ 2\cdot (p - p_v ) }{ Ca \cdot v^2 }\) \( v \;=\; \sqrt{ \dfrac{ 2\cdot (p - p_v ) }{ Ca \cdot \rho } }\) |
||
| Symbol | English | Metric |
| \( Ca \) = Cavitation Number | \( dimensionless \) | \( dimensionless \) |
| \( p \) = Local Static Pressure | \(lbf \;/\; in^2\) | \(Pa\) |
| \( p_v \) = Fluid Vapor Pressure at a Given Temperature | \(lbf \;/\; in^2\) | \(Pa\) |
| \( \rho \) (Greek symbol rho) = Fluid Density | \(lb \;/\; ft^3\) | \(kg \;/\; m^3\) |
| \( U \) = Flow Velocity | \(ft \;/\; sec\) | \(m \;/\; s\) |
Cavitation number, abbreviated Ca or \(\sigma\) (Greek symbol sugma), a dimensionless number, expresses the relationship between the difference of a local absolute pressure from the vapor pressure and the kinetic energy per volume.
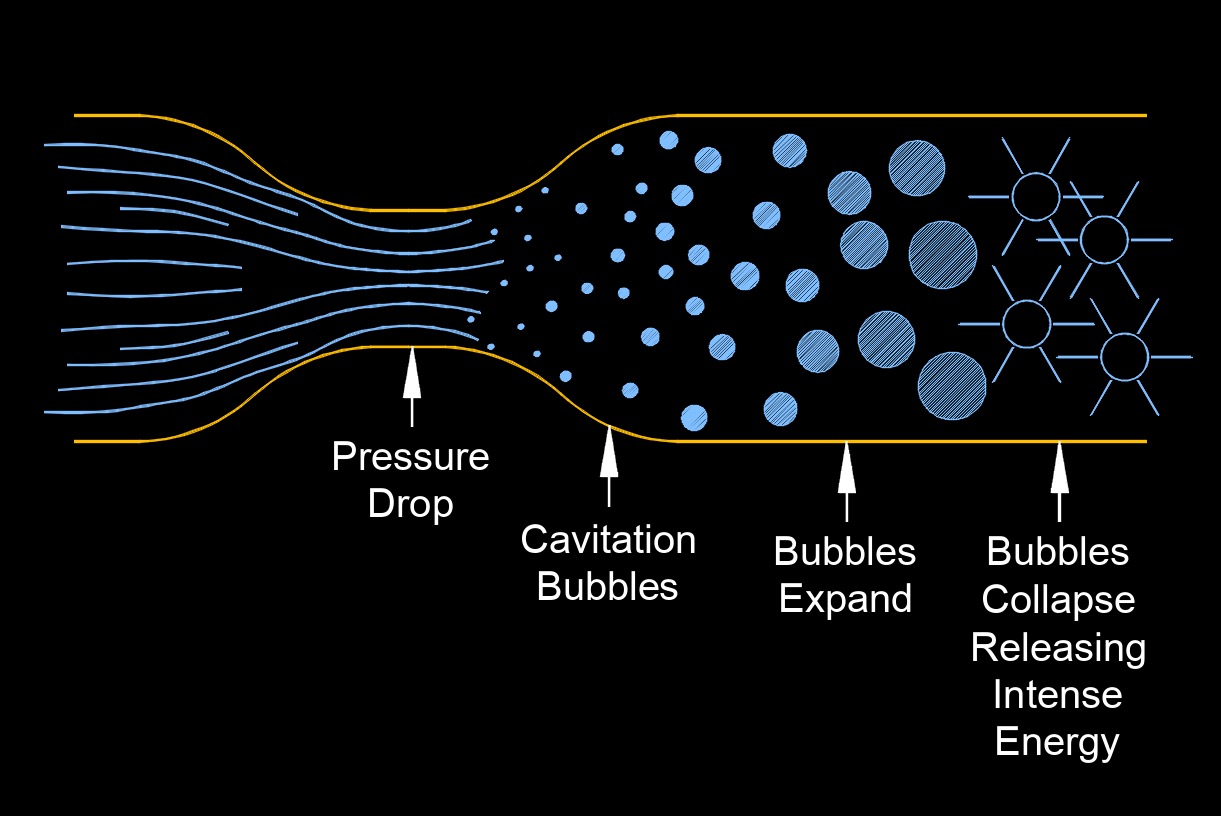
The cavitation number is used in fluid dynamics to characterize the potential for cavitation to occur in a flowing fluid. Cavitation refers to the formation and subsequent collapse of vapor bubbles in a liquid due to a decrease in pressure below the vapor pressure of the liquid. The cavitation number represents the ratio of the pressure drop to the kinetic energy in the fluid flow. It provides a measure of the relative importance of the pressure change compared to the fluid's kinetic energy. When the cavitation number is less than 1, the fluid flow is considered to be at risk of cavitation.
If the cavitation number is close to or below 1, the fluid pressure can drop below the vapor pressure, causing the formation of vapor bubbles. These bubbles can subsequently collapse violently, leading to damage to equipment and undesirable effects such as noise, erosion, and loss of efficiency in hydraulic systems, pumps, propellers, and other fluid flow applications.
Cavitation Number Interpretation
- Very Low Cavitation Number (Ca << 1 or even negative) - This signifies a situation where the local pressure is very close to or even below the vapor pressure. This strongly indicates that cavitation will occur and is likely to be intense.
- Low Cavitation Number (Ca ≈ 1 or << 1) - The dynamic pressure is significant relative to the pressure margin above the vapor pressure. This means the local pressure can easily drop below PvPv in high-velocity regions (like around a propeller blade or in a pump), leading to cavitation. Bubbles form, collapse, and can cause noise, vibration, or erosion.
- High Cavitation Number (Ca >> 1) - The local pressure is well above the vapor pressure compared to the dynamic pressure. Cavitation is unlikely because the pressure drop caused by the flow isn’t enough to reach the vaporization threshold. The system is "safe" from bubble formation.
Cavitation Number Significance
The cavitation number is important in the design and analysis of fluid systems, such as pumps, propellers, and valves, where cavitation can have detrimental effects on performance and equipment durability. Engineers use the cavitation number to assess the potential for cavitation in a given fluid flow and make design decisions to prevent or mitigate its effects.
