Vapor Pressure
Vapor pressure, abbreviated as pv, of a substance is the pressure at a certain temperature when the liquid and vapor are in equilibrium. Liquid vapor pressure is measured in the laboratory at 100 degrees fahrenheit and is referred to as the Reed Vapor Pressure. As the temperature of a liquid increases, the vapor pressure also increases.
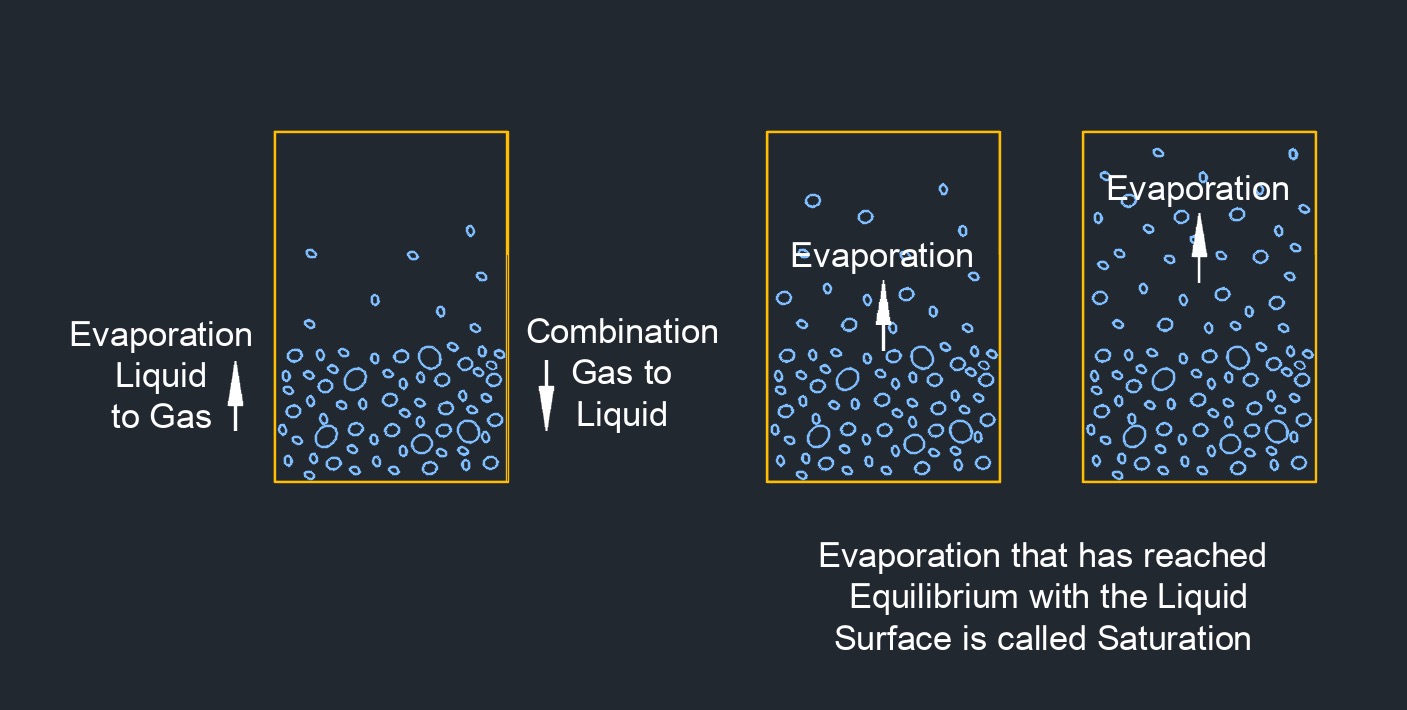
Boiling point is the temperature at which the vapor pressure equals atmospheric pressure. In engineering, the vapor pressure is extremely important when sizing pumps. When there is low net positive suction head available \(NPSHa\), vapor pressure can play a large role in preventing (or assisting in) cavitation.
- See Article - Properties of Hydrocarbon Gasses
Vapor Pressure formula |
||
|
\( p_v \;=\; x_s \; p_{v}{^o} \) (Vapor Pressure) \( x_s \;=\; p_v \;/\; p_{v}{^o} \) \( p_{v}{^o} \;=\; p_v \;/\; x_s \) |
||
| Symbol | English | Metric |
| \( p_v \) = Vapor Pressure (psi) | \(lbf\;/\;in^2\) | \(Pa\) |
| \( x_s \) (Greek symbol chi) = Solution Mole Fraction | \( dimensionless \) | \( dimensionless \) |
| \( p_{v}{^o} \) = Pure Solution Vapor Pressure (psi) | \(lbf\;/\;in^2\) | \(Pa\) |
