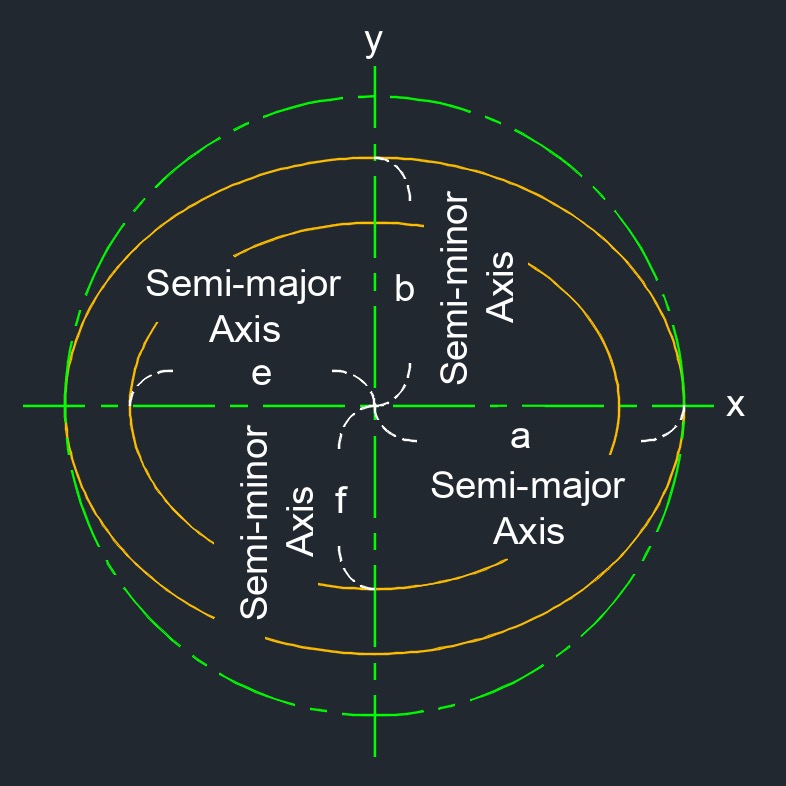
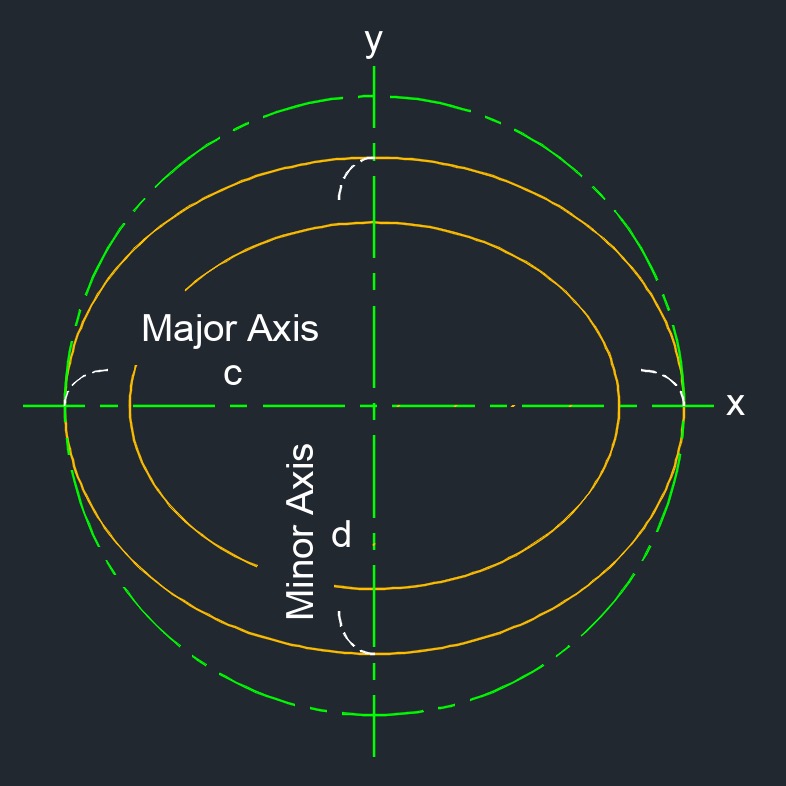
Hollow Ellipse

Hollow ellipse (a two-dimensional figure) has two ellipses with a conic section or a stretched circle.
The major axis is always the longest axis in an ellipse.
The minor axis is always the shortest axis in an ellipse.

Area of a Hollow ellipse formula
$A_{area} \;=\; \pi \cdot ( a \cdot b - e \cdot f )$
Symbol	English	Metric
$A$ = area	$in^2$	$mm^2$
$a$ = length semi-major axis	$in$	$mm$
$b$ = length semi-minor axis	$in$	$mm$
$e$ = length inner semi-major axis	$in$	$mm$
$f$ = length inner semi-minor axis	$in$	$mm$
$\pi$ = Pi	$3.141 592 653 ...$	$3.141 592 653 ...$

Inner Semi-major Axis Length of a Hollow ellipse formula
$e \;=\; a - g$
Symbol	English	Metric
$a$ = length semi-major axis	$in$	$mm$
$b$ = length semi-minor axis	$in$	$mm$
$g$ = ring width	$in$	$mm$

Inner Semi-minor Axis Length of a Hollow ellipse formula
$f \;=\; b - g$
Symbol	English	Metric
$a$ = length semi-major axis	$in$	$mm$
$b$ = length semi-minor axis	$in$	$mm$
$g$ = ring width	$in$	$mm$