Skip to main content

Trig Functions

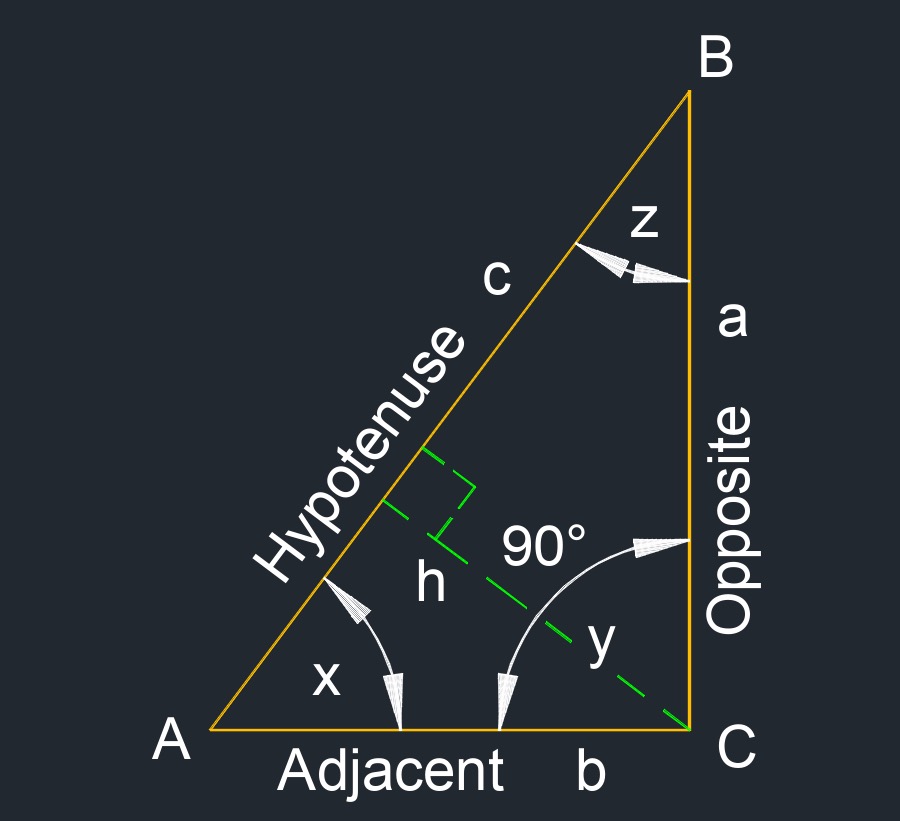Trigonometric functions, also called trig functions, are mathematical functions that relate the angles of a right triangle to the ratios of the sides.  These functions are fundamental in trigonometry and have applications in various fields, including physics, engineering, computer science, and more.  They are often used to model periodic phenomena, such as oscillations and waves, and are crucial in solving problems involving angles and triangles.  Additionally, trigonometric functions play a significant role in calculus and complex number theory.

  • Hypotenuse  -  The side opposite the right angle "C", is the hypotenuse "c".
  • Opposite Leg  -  The side opposite to the angle needed "A", is the opposite side "a".
  • Adjacent Leg  -  The side opposite the hypotenuse and next to the angle needed, is the adjacent side "b".

 

Trig abbreviations

\(\large{ \ sine = sin }\)

\(\large{ \ cosine = cos }\)

\(\large{ \ tangent = tan }\)

\(\large{ \ cotangent = cot }\)

\(\large{ \ cosecant = csc }\)

\(\large{ \ secant = sec }\)

\(\large{ \ arcsine = arcsin }\)

\(\large{ \ arccosine = arccos }\)

\(\large{ \ arctangent = arctan }\)

\(\large{ \ arccotangent = arccot }\)

\(\large{ \ arccosecant = arccsc }\)

\(\large{ \ arcsecant = arcsec }\)

  

Trig Functions formulas

\(\large{ \ sin \; \theta= \frac {opposite}{hypotenuse} }\)   

\(\large{ \ cos \; \theta= \frac {adjacent}{hypotenuse} }\)  

\(\large{ \ tan \; \theta= \frac {opposite}{adjacent} }\)  

\(\large{ \ csc \; \theta= \frac {hypotenuse}{opposite} }\) 

\(\large{ \ sec \; \theta= \frac {hypotenuse}{adjacent} }\)

\(\large{ \ cot \; \theta= \frac {adjacent}{opposite} }\)  

\(\large{ \ arcsin \; \theta= \frac {opposite}{hypotenuse} }\) 

\(\large{ \ arccos \; \theta= \frac {adjacent}{hypotenuse} }\)

\(\large{ \ arctan \; \theta= \frac {opposite}{adjacent} }\)

\(\large{ \ arccsc \; \theta= \frac {hypotenuse}{opposite} }\)

\(\large{ \ arcsec \; \theta= \frac {hypotenuse}{adjacent} }\)

\(\large{ \ arccot \; \theta= \frac {adjacent}{opposite} }\)

  

Trig Functions Equations
Find p
  • given a b c :  \(\; p= a+b+c \)
Find s
  • given a b c :  \(\; s= (a+b+c) \div 2 \)
Find d
  • given a b c s :  \(\; d= (b^2+c^2-a^2) \div 2b \)
Find e
  • given a b c s :  \(\; e= (a^2+b^2-c^2) \div 2b \)
Find h
  • given c A :  \(\; h= c*sin \;A \)
  • given a C :  \(\; h= a*sin \;C \)
Find Area
  • given a b c :  \(\; A_{area}=\frac {1}{2}(bh) \)
  • given a b c :  \(\; A_{area}=  \sqrt { s(s-a)(s-b)(s-c) } \)
  • given C a b :  \(\; A_{area}= \frac{1}{2} ab* \sin \; c \)
Find A
  • given a b c s :  \(\; \sin \frac{1}{2} A=  \sqrt {(s-b)(s-c) \div bc } \)
  • given a b c s :  \(\; \cos \frac{1}{2} A= \sqrt {s(s-a) \div bc } \)
  • given a b c s :  \(\; \tan \frac{1}{2} A= \sqrt {(s-b)(s-c) \div s(s-a) } \)
  • given c h :  \(\;\ sin \; A= \frac {h}{c} \)
  • given B a b :  \(\;\ sin \; A= a* sin\; B \div b \)
  • given B a c :  \(\; A= \frac{1}{2}(A+C)+\frac{1}{2}(A-C) \)
  • given C a b :  \(\; A= \frac{1}{2}(A+B)+\frac{1}{2}(A-B) \)
  • given C a c :  \(\;\ sin \; A= a* sin \; C \div c \)
Find B
  • given a b c s :  \(\; \sin \frac{1}{2} B= \sqrt {(s-a)(s-c) \div ac} \)
  • given a b c s :  \(\; \cos \frac{1}{2} B= \sqrt {s(s-b) \div ac} \)
  • given a b c s :  \(\; \tan \frac{1}{2} B= \sqrt {(s-a)(s-c) \div s(s-b)} \)
  • given a h :  \(\;\ sin \; B= \frac {h}{a} \)
  • given A a b :  \(\;\ sin B= b* sin \; A \div a \)
  • given A b c :  \(\;\ B= \frac{1}{2}(B+C)+\frac{1}{2}(B-C) \)
  • given C a b :  \(\; B= \frac{1}{2}(A+B)-\frac{1}{2}(A-B) \)
  • given C a c :  \(\;\ sin \; B= b* sin \; C \div c \)
Find C
  • given a b c s :  \(\; \sin \frac{1}{2} C= \sqrt {(s-a)(s-b) \div ab} \)
  • given a b c s :  \(\; \cos \frac{1}{2} C= \sqrt {s(s-c) \div ab} \)
  • given a b c s :  \(\; \tan \frac{1}{2} C= \sqrt {(s-a)(s-b) \div s(s-c) } \)
  • given A a c :  \(\;\ sin \; C= c* sin \; A \div a \)
  • given A b c :  \(\; C= \frac{1}{2}(B+C)-\frac{1}{2}(B-C) \)
  • given B a c :  \(\; C= \frac{1}{2}(A+C)-\frac{1}{2}(A-C) \)
  • given B b c :  \(\;\ sin \; C= c* sin \; B \div c \)
Find a
  • given A B b :  \(\; a= b* \sin \; A \div \sin \; B \)
  • given A B c :  \(\; a= c* \sin \; A \div \sin (A+B) \)
  • given A C b :  \(\; a= b* \sin \; A \div \sin (A+C) \)
  • given A C c :  \(\; a= c* \sin \; A \div \sin \; C \)
  • given B C b :  \(\; a= b* \sin (A+C) \div \sin \; B \)
  • given B C c :  \(\; a= c* \sin (A+C) \div \sin \; C \)
  • given A b c :  \(\; a= \sqrt {b^2+c^2-2bc * \cos \; A} \)
Find b
  • given A B a :  \(\; b= a* \sin \; B \div \sin \; A \)
  • given A B c :  \(\; b= c* \sin \; B \div \sin (A+B) \)
  • given A C a :  \(\; b= a* \sin (A+C) \div \sin \; A \)
  • given A C c :  \(\; b= c* \sin (A+C) \div \sin \; C \)
  • given B C a :  \(\; b= a* \sin \; B \div \sin (B+C) \)
  • given B C c :  \(\; b= c* \sin \; B \div \sin \; C \)
  • given B a c :  \(\; b= \sqrt {a^2+c^2-2ac * \cos B} \)
Find c
  • given A B a :  \(\; c= a* \sin (A+B) \div \sin \; A \)
  • given A B b :  \(\; c= b* \sin (A+B) \div \sin \; B \)
  • given A C a :  \(\; c= a* \sin \; C \div \sin \; A \)
  • given A C b :  \(\; c= b* \sin \; C \div \sin (A+C) \)
  • given B C a :  \(\; c= a* \sin \; C \div \sin (B+C) \)
  • given B C b :  \(\; c= b* \sin \; C \div \sin \; B \)
  • given C a b :  \(\; c= \sqrt {a^2+b^2-2ab * \cos \; C} \)

 

Piping Designer Logo 1