Reservoir Fluid Permeability Formula |
||
|
\( k \;=\; \dfrac{ \eta \cdot V \cdot P_l }{ A_p \cdot p_g \cdot t }\) (Reservoir Fluid Permeability) \( \eta \;=\; \dfrac{ k \cdot A_p \cdot p_g \cdot t }{ V \cdot P_l }\) \( V \;=\; \dfrac{ k \cdot A_p \cdot p_g \cdot t }{ \eta \cdot P_l }\) \( P_l \;=\; \dfrac{ k \cdot A_p \cdot p_g \cdot t }{ \eta \cdot V }\) \( A_p \;=\; \dfrac{ \eta \cdot V \cdot P_l }{ k \cdot p_g \cdot t }\) \( p_g \;=\; \dfrac{ \eta \cdot V \cdot P_l }{ k \cdot A_p \cdot t }\) \( t \;=\; \dfrac{ \eta \cdot V \cdot P_l }{ k \cdot A_p \cdot p_g }\) |
||
| Symbol | English | Metric |
| \( k \) (Greek symbol mu) = Medium Permeability | \(ft^2\) | \(m^2\) |
| \( \eta \) (Greek symbol eta) = Viscosity of Liquid Phase | \(lbf - sec \;/\; ft^2\) | \( Pa - s \) |
| \( V \) = Liquid Volume that Flows in Time - Burette Volume | \(in^3\) | \(cm^3\) |
| \( P_l \) = Plug Length | \(in\) | \(cm\) |
| \( A_p \) = Plug Open Flow Area | \(in^2\) | \(cm^2\) |
| \( p_g \) = Pressure Value from Pressure Gauge (psi) | \(lbf \;/\; in^2\) | \(Pa\) |
| \( t \) = Flow Time | \(sec\) | \(s\) |
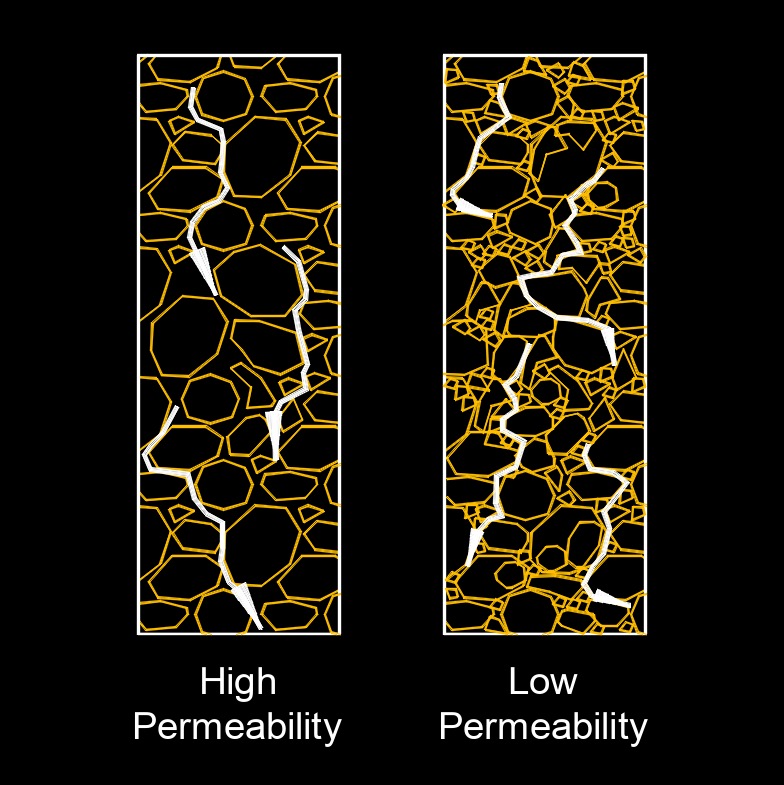Reservoir fluid permeability, abbreviated as \( k \) (Greek symbol mu), is a measure of the ability of a porous material (such as rock in a reservoir) to allow fluids (such as oil, gas, or water) to pass through it. It is used in petroleum engineering and hydrogeology for understanding and predicting fluid flow in reservoirs. The higher the permeability, the more easily fluids can flow through the rock. Permeability is usually determined through laboratory measurements on core samples or inferred from well tests and log data. Understanding permeability is essential for efficient reservoir management and for optimizing the extraction of hydrocarbons.
