Buoyant Unit Weight Formula
|
|
\( \gamma ' \;=\; \gamma_{sat} - \gamma_w \) (Buoyant Unit Weight)
\( \gamma_{sat} \;=\; \gamma ' + \gamma_w \)
\( \gamma_w \;=\; \gamma_{sat} - \gamma ' \)
|
| Symbol |
English |
Metric |
| \( \gamma ' \) (Greek symbol gamma) = Buoyant Unit Weight |
\( lbm \;/\; ft^3 \) |
\( N \;/\; m^3 \) |
| \( \gamma_{sat} \) (Greek symbol gamma) = Saturated Unit Weight |
\( lbm \;/\; ft^3 \) |
\( N \;/\; m^3 \) |
| \( \gamma_w \) (Greek symbol gamma) = Unit Weight of Water |
\( lbm \;/\; ft^3 \) |
\( N \;/\; m^3 \) |
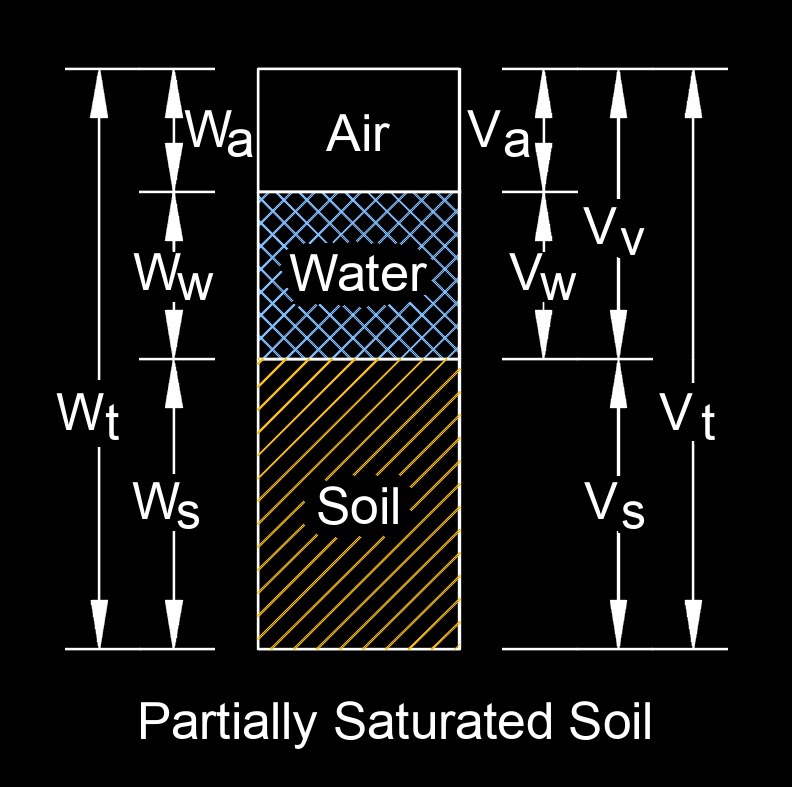 Buoyant unit weight, abbreviated as \( \gamma ' \), also called effective unit weight or submerged unit weight, is a measure of the effective weight of a substance (usually a soil or a material) when it is submerged or floating in a fluid, typically water. It is an important concept in the field of soil mechanics and geotechnical engineering, as well as in fluid mechanics.
Buoyant unit weight, abbreviated as \( \gamma ' \), also called effective unit weight or submerged unit weight, is a measure of the effective weight of a substance (usually a soil or a material) when it is submerged or floating in a fluid, typically water. It is an important concept in the field of soil mechanics and geotechnical engineering, as well as in fluid mechanics.
The buoyant unit weight takes into account the weight of the material itself and the buoyant force exerted on it by the surrounding fluid. When an object is submerged in a fluid, it experiences an upward force called buoyancy, which counteracts the force of gravity. This is described by Archimedes' principle. The buoyant unit weight is particularly relevant in geotechnical engineering when dealing with submerged soils or materials, as it helps engineers assess the stability and behavior of structures like dams, foundations, and retaining walls that are in contact with water or are submerged in water.


 Buoyant unit weight, abbreviated as \( \gamma ' \), also called effective unit weight or submerged unit weight, is a measure of the effective weight of a substance (usually a soil or a material) when it is submerged or floating in a fluid, typically water. It is an important concept in the field of soil mechanics and
Buoyant unit weight, abbreviated as \( \gamma ' \), also called effective unit weight or submerged unit weight, is a measure of the effective weight of a substance (usually a soil or a material) when it is submerged or floating in a fluid, typically water. It is an important concept in the field of soil mechanics and 